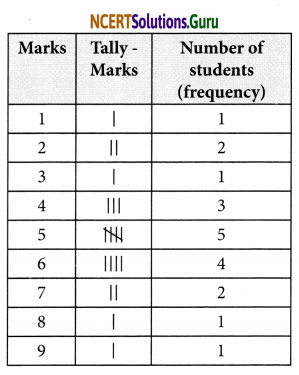
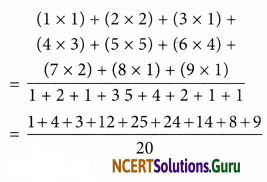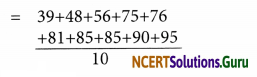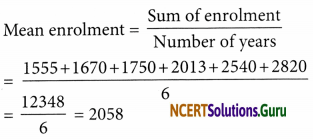NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.3
These NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.3 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Exercise 3.3
Question 1.
Use the bar graph to answer the following questions.
Data Handling
(a) Which is the most popular pet?
(b) How many students have dog as a pet?

Answer:
(a) Since the bar representing 10 is the longest, the most popular pet is cat.
(b) 8 students have dog as a pet.
![]()
Question 2.
Read the bar graph which shows the number of books sold by a book store
during five consecutive years and answer the following questions:
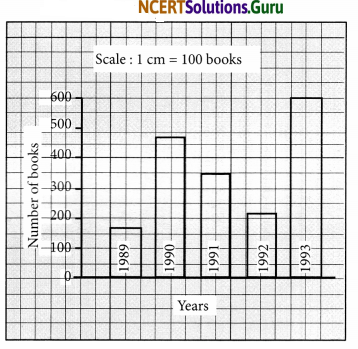
(i) About how many books were sold in 1989? 1990? 1992?
(ii) In which year were about 475 books sold? About 225 books sold?
(iii) In which years were fewer than 250 books sold?
(iv) Can you explain how you would estimate the number of books sold in 1989?
Answer:
(i) Number of books sold:
In 1989 were about 180
In 1990 were about 475
In 1992 were about 225
(ii) About 475 books were sold in 1990 and about 225 books were sold in 1992.
(iii) Fewer than 250 books were sold in 1989 and 1992.
(iv) The height of the bar for 1989 is slightly less than that for 200 books.
Therefore, about 180 books were sold in 1989.
![]()
Question 3.
Number of children in six different classes are given below. Represent the data on a bar graph.
| Class | Number of Children |
| Fifth | 135 |
| Sixth | 120 |
| Seventh | 95 |
| Eighth | 100 |
| Ninth | 90 |
| Tenth | 80 |
(a) How would you choose a scale?
(b) Answer the following questions:
(i) Which class has the maximum number of children? And the minimum?

(ii) Find the ratio of students of class sixth to the students of class eighth.
Answer:
(a) Start the scale at 0. The greatest value in the data is 135, so end the scale at a
value greater than 135 such as 140.
Use equal divisions along the axes such as increment of 10.
(i) We know that all the bars would lie between 0 and 140.
(ii) We choose the scale such that the length between 0 and 140 is neither too long nor too small.
(iii) Here we take one unit for 10 children.
(b) (i) Fifth class has the maximum number of children. Tenth class has the minimum number of
children.
(ii) Ratio of students of class sixth to
Eighth = 120 : 100 = 12 : 10 = 6 : 5
![]()
Question 4.
The performance of a student in 1st Term and 2nd Term is given. Draw a double bar graph choosing appropriate scale and answer the following:

(i) In which subject, has the child improved his performance the most?
(ii) In which subject is the improvement the least?
(iii) Has the performance gone down in any subject?
Answer:
The required double bar graph is given below:

This graph shows the performance of students in st term and 2nd term.
(i) The child improved his performance the most in Maths.
(ii) The improvement is the least in the subject of social science.
(iii) Yes, the performance has gone down in the subject of Hindi.
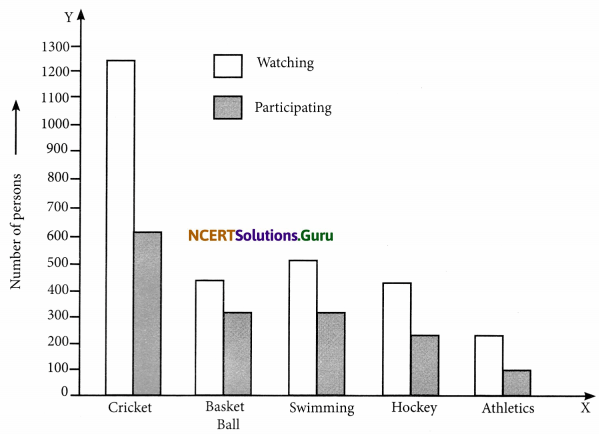
Question 5.
Consider this data collected from a survey of a colony.

(i) Draw a double bar graph choosing an appropriate scale.
What do you infer from the bar graph?
(ii) Which sport is most popular?
(iii) Which is more preferred, watching or participating in sports?
Answer:
(i) The required ‘double bar graph’ is given below :
From the bar graph it is inferred that the people of the colony like cricket the most and athletics the least.
(ii) The most popular sport is cricket.
(iii) Watching sports is more preferred than participating in sports.
![]()
Question 6.
Take the data giving the minimum and the maximum temperature of various cities given in the beginning of this Chapter. Plot a double bar graph using the data and answer the following:
(i) Which city has the largest difference in the minimum and maximum temperature on the given date?
(ii) Which is the hottest city and which is the coldest city?
(iii) Name two cities where maximum temperature of one was less than the minimum temperature of the other.
(iv) Name the city which has the least difference between its minimum and the maximum temperature.
Temperature of cities as on 20.06.2006
| City | Maximum | Minimum |
| Ahmedabad | 38°C | 29°C |
| Amritsar | 37°C | 26°C |
| Bengaluru | 28°C | 21°C |
| Chennai | 36°C | 27°C |
| Delhi | 38°C | 28°C |
| Jaipur | 39°C | 29°C |
| Jammu | 41°C | 26°C |
| Mumbai | 32°C | 27°C |
Answer:
Plotting a double bar graph, we get.
City Difference in the minimum and maximum temperature on 20-06-2006
| City | Difference in the minimum and maximum temperature on 20-06-2006 |
| Ahmedabad | 38°C – 29°C = 9°C |
| Amritsar | 37°C – 26°C = trC |
| Bengaluru | 28°C – 21°C = 7°C |
| Chennai | 36°C – 27°C = 9°C |
| Delhi | 38°C – 28°C = 10°C |
| Jaipur | 39°C – 29°C = 10°C |
| Jammu | 41°C – 26°C = 15°C |
| Mumbai | 32°C – 27°C = 5°C |
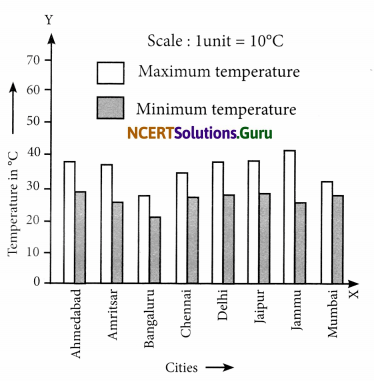
(i) Jammu has the largest difference in the minimum and maximum temperatures on the given data.
(ii) Jammu is the hottest city and Bengaluru is the coldest city.
(iii) Bangaluru and Jaipur or Bengaluru and Ahmedabad.
(iv) Mumbai has the least difference between its maximum temperature and minimum temperature.
NCERT Solutions for Class 7 Maths Chapter 3 Data Handling Ex 3.3 Read More »