CBSE Class 7

These NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Exercise 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if ……………….
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is ……………….
(c) When we write ∠A = ∠B, we actually mean …………………
Answer:
(a) Two line segments are congruent if they have the same length.
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is 70°.
(c) When we write ∠A ≅ ∠B we actually mean m ∠A = m ∠B.

Question 2.
Give any two real-life examples for congruent shapes.
Answer:
(i) Two ten-rupee notes.
(ii) Biscuits of the same type in the same packet.

Question 3.
If ΔABC ≅ ΔFED under the correspondences ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Answer:
Corresponding vertices : A and F; B and E; C and D.

Corresponding sides : \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{FE}} ; \overline{\mathrm{BC}}\) and \overrightarrow{\mathrm{ED}} ; \overline{\mathrm{CA}} and \(\overline{\mathrm{AB}}\)

Corresponding angles : ∠A and ∠F; ∠B and ∠E; ∠C and ∠D

Question 4.
If ΔDEF ≅ ΔBCA, write the part (s) of ΔBCA that correspond to
(i) ∠E
(ii) \(\overline{\mathrm{EF}}\)
(iii) ∠F
(iv) \(\overline{\mathrm{DF}}\)
Answer:
(i) ∠C
(ii) \(\overline{\mathrm{CA}}\)
(iii) ∠A
(iv) \(\overline{\mathrm{BA}}\)

These NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers InText Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers InText Questions

NCERT In-text Question Page No. 174

Question 1.
Is the number \(\frac{2}{-3}\) rational? Think about it.
Answer:
Yes, \(\frac{2}{-3}\) is a rational number,
∵ 2 and -3 are integers and -3 ≠ 0.

Question 2.
List ten rational numbers.
Answer:
Following are ten rational numbers:
\(\frac{1}{3}, \frac{-2}{3}, \frac{4}{5}, \frac{1}{-6}, \frac{-3}{-4}, 5.8,2 \frac{4}{5}\), 0.93, 18 and 11.07
Note: 1. ‘0’ can be written as \(\frac{0}{2}\) or \(\frac{0}{15}\) etc.
Hence, it is a rational number.
2. A natural number can be written as
5 = \(\frac{5}{1}\) or 108 = \(\frac{108}{1}\) Hence, it is also a rational number.

NCERT In-text Question Page No. 175

Question 1.
Fill in the boxes:

Answer:

Question 2.
Is 5 a positive rational number?
Answer:
Yes, 5 or \(\frac{5}{1}\) is having both its numerator
and denominator as positive.
∴ It is a positive rational number.

Question 3.
List five more positive rational numbers.
Answer:
\(\frac{1}{7}, \frac{3}{8}, \frac{5}{17}, \frac{2}{9}\) and \(\frac{5}{18}\) and are positive rational numbers.

NCERT In-text Question Page No. 176

Question 1.
Is -8 a negative rational number?
Answer:
(i) Yes, -8 or \(\frac{-8}{1}\) is a negative rational number, because its numerator is a negative integer.

Question 2.
List five more negative rational numbers.
Answer:
Five negative rational numbers are as follows:
\(\frac{-5}{9}, \frac{-6}{11}, \frac{-3}{13}, \frac{3}{-10} \text { and } \frac{-1}{7}\)

Question 3.
Which of these are negative rational numbers?
(i) \(\frac{-2}{3}\)
(ii) \(\frac{5}{7}\)
(iii) \(\frac{3}{-5}\)
(iv) 0
(v) \(\frac{6}{11}\)
(vi) \(\frac{-2}{-9}\)
Answer:
(i) \(\frac{-2}{3}\) is a negative rational number.
(ii) \(\frac{5}{7}\) is a positive rational number.
(iii) \(\frac{3}{-5}\) is a negative rational number.
(iv) 0 is neither a positive nor a negative rational number.
(v) \(\frac{6}{11}\) is a positive rational number.
(vi) \(\frac{-2}{-9}\) is a positive rational number.
∴ (i) \(\frac{-2}{3}\) and (ii) \(\frac{3}{-5}\) are negative rational numbers.

NCERT In-text Question Page No. 178

Question 1.
Find the standard form of:
(i) \(\frac{-18}{45}\)
(ii) \(\frac{-12}{18}\)
Answer:
(i) Since HCF of 18 and 45 is 9.
∴ \(\frac{-18}{45}=\frac{(-18) \div 9}{45 \div 9}=\frac{-2}{5}\)
Thus, the standard form of \(\frac{-18}{45}\) is \(\frac{-2}{3}\)

(ii) Since HCF of 12 and 18 is 6.
∴ \(\frac{-12}{18}=\frac{(-12) \div 6}{18 \div 6}=\frac{-2}{3}\)
Thus, the standard form of \(\frac{-12}{18}\) is \(\frac{-2}{3}\)

NCERT In-text Question Page No. 181

Question 1.
Find five rational numbers between \(\frac{-5}{7}\) and \(\frac{-3}{8}\)
Answer:
First we convert the given rational numbers with common denominators,
∴ LCM of 7 and 8 is 56.

Thus, the five rational numbers, between \(\frac{-5}{7}\) and \(\frac{-3}{8}\) are:

NCERT In-text Question Page No. 185

Question 1.
Find:
(i) \(\frac{-13}{7}+\frac{6}{7}\)
(ii) \(\frac{-19}{5}+\frac{-7}{5}\)
Answer:

Question 2.
Find:
(i) \(\frac{-3}{7}+\frac{2}{3}\)
(ii) \(\frac{-5}{6}+\frac{-3}{11}\)
Answer:
(i) \(\frac{-3}{7}+\frac{2}{3}\)
∴ LCM of 7 and 3 is 21

NCERT In-text Question Page No. 186

Question 1.
What will be the additive inverse of \(\frac{3}{9} ?, \frac{-9}{11} ?, \frac{5}{7} ?\)
Answer:
Additive inverse of \(\frac{-3}{9}\) is \(\frac{3}{9}\).
Additive inverse of \(\frac{-9}{11}\) is \(\frac{9}{11}\).
Additive inverse of \(\frac{5}{7}\) is \(\frac{-5}{7}\).

NCERT In-text Question Page No. 187

Question 1.
Find
(i) \(\frac{7}{9}-\frac{2}{5}\)
(ii) \(2 \frac{1}{5}-\left(\frac{-1}{3}\right)\)
Answer:
(i) \(\frac{7}{9}-\frac{2}{5}\)
L.C.M of 9 and 5 is 45.

(ii) \(2 \frac{1}{5}-\left(\frac{-1}{3}\right)\)
L.C.M of 5 and 3 is 15.

NCERT In-text Question Page No. 188

Question 1.
What will be
(i) \(-\frac{3}{5} \times 7\)
(ii) \(-\frac{6}{5} \times(-2) ?\)
Answer:
(i) \(-\frac{3}{5} \times 7=\frac{(-3) \times 7}{5}=\frac{-21}{5}=-4 \frac{1}{5}\)
(ii) \(\frac{-6}{5} \times(-2)=\frac{(-6) \times(-2)}{5}=\frac{12}{5}=2 \frac{2}{5}\)

Question 2.
(i) \(\frac{-3}{4} \times \frac{1}{7}\)
(ii) \(\frac{2}{3} \times \frac{-5}{9}\)
Answer:
(i) \(\frac{-3}{4} \times \frac{1}{7}=\frac{-3 \times 1}{4 \times 7}=\frac{-3}{28}\)
(ii) \(\frac{2}{3} \times \frac{-5}{9}=\frac{-2 \times 5}{3 \times 9}=\frac{-10}{27}\)

NCERT In-text Question Page No. 189

Question 1.
What wTill be the reciprocal of \(\) and \(\) ?
Answer:
Reciprocal of \(\frac{-6}{11}\) is \(\frac{-11}{6}\)
Reciprocal of \(\frac{-8}{5}\) is \(\frac{-5}{8}\)

NCERT In-text Question Page No. 190

Question 1.
Find
(i) \(\frac{2}{3} \times \frac{-7}{8}\)
(ii) \(\frac{-6}{7} \times \frac{5}{7}\)
Answer:
(i) \(\frac{2}{3} \times \frac{-7}{8}=\frac{-7}{12}\)
(ii) \(\frac{-6}{7} \times \frac{5}{7}=\frac{-30}{49}\)

These NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties InText Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties InText Questions

NCERT In-text Question Page No. 113 & 114
Question 1.
Write the six elements (i.e. the 3 sides and the 3 angles) of ΔABC.
Answer:
Six elements of ΔABC are: ∠A, ∠B, ∠C, \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), and \(\overline{\mathrm{CA}}\).

Question 2.
Write the:
(i) Side opposite to the vertex Q of ΔPQR
(ii) Angle opposite to the side LM of ΔLMN
(iii) Vertex opposite to the side RT of ΔRST
Answer:
(i) The side opposite to the vertex Q is \(\overline{\mathrm{PR}}\).

(ii) The angle opposite to the side LM is ∠N.

(iii) Vertex opposite to the side RT is ‘S’.

Question 3.
Look at figures and classify each of the triangles according to its.
(a) Sides
(b) Angles

Answer:
(i) (a) Since \(\overline{\mathrm{AC}}=\overline{\mathrm{BC}}\) = 8 cm
∴ ΔABC is an isosceles triangle,

(b) Since all angles of ∴ABC are less than 90°.
∴ It is an acute triangle.

(ii) (a) Since PQ ≠ QR ≠ RP
∴ ΔPQR is a scalene triangle.

(b) Since ∠R = 90°
∴ ΔPRQ is a right triangle.

(iii) (a) In ΔLMN, LN = MN = 7 cm
∴ ΔLMN is an isosceles triangle,

(b) In ΔLMN, ∠N > 90°
∴ ΔLMN is an obtuse triangle.

(iv) (a) In ΔRST, RS = ST = TR = 5.2 cm
∴ It is an equilateral triangle.

(b) All the angles of ΔRST are acute.
∴ It is an acute triangle.

(v) (a) In ΔABC, \(\overline{\mathrm{AB}}=\overline{\mathrm{BC}}\) = 3 cm
∴ It is an isosceles triangle.

(b) In ΔABC, ∠B > 90°
∴ It is an obtuse triangle.

(vi) (a) In ΔPQR, latex]\overline{\mathrm{PQ}}=\overline{\mathrm{QR}}[/latex] = 6 cm
∴ It is an isosceles triangle.

(b) In ΔPQR, ∠Q = 90°
∴ It is a right triangle.

NCERT In-text Question Page No. 118
Question 1.
An exterior angle of a triangle is of measure 70° and one of its interior opposite angles is for measure 25°. Find the measure of the other interior opposite angle.
Answer:
Exterior angle = 70°
Interior opposite angles are 25° and x.
∴ x + 25° = 70°
[Using the exterior angle property of a triangle]
or x = 70°- 25°= 45°
∴ The required interior opposite angle = 45°.

Question 2.
The two interior opposite angles of an exterior angle of triangle are 60° and 80°. Find the measure of the exterior angle.
Answer:
Interior angles are 60° and 80°.
∵ [Exterior angle] = 60° + 80° = 140°

Question 3.
Is something wrong in this diagram?

Answer:
We know that an exterior angle of a triangle is equal to the sum of interior opposite angles. Here interior angles are 50° each and exterior angle is 50°.
∴ This triangle cannot be formed.
[∵ 50° ≠ 50° + 50°]

NCERT In-text Question Page No. 122
Question 1.
Two angles of a triangle are 30° and 80°. Find the third angle.
Answer:
Let the third angle be x.
∴ Using the angle sum property of a triangle,
30° + 80° + x = 180°
or x + 110° = 180°
or x = 180°- 110° = 70°
∴ The measure of the required third angle is 70°.

Question 2.
One of the angles of a triangle is 80° and the other two angles are equal. Find the measure of each of the equal angles.
Answer:
Let each of the equal angles be x
x + x + 80° = 180°
(angle sum property of a triangle)
2x + 80° = 180°
2x = 180° – 80°
2x = 100°
x = \(\frac{100^{\circ}}{2}\) = 50°
∴ The required measure of each of the equal angle is 50°.

Question 3.
The three angles of a triangle are in the ratio 1:2:1. Find all the angles of the triangle. Classify the triangle in two different ways.
Answer:
Let the three angles of a triangle be x, 2x and x
x + 2x + x = 180°
(using the angle sum property)
2x + 2x = 180°
4x = 180°
x \(\frac{180^{\circ}}{4}\) = 45°
Thus, the three angles are 45°, 90° and 45°. It is an isosceles triangle (two angles are equal, opposite sides also equal)
As one angle is 90°.
∴ It is a right-angled triangle.

NCERT In-text Question Page No. 123 & 124
Question 1.
Find angle x in each figure:





Answer:
(i) Since the two sides in the triangle are equal, the base angle opposite to equal sides are equal.
∴ x = 40°

(ii) Since the two sides of the triangle are equal, the base angles opposite to equal sides are equal so, the other angle = 45°
Sum of three angles of a triangle = 180°
45° + 45° + x = 180°
x + 90° = 180°
x = 180° – 90°
x = 90°

(iii) Since the two sides of the triangle are equal, the base angles opposite to equal sides are equal.
x = 50°

(iv) Base angles opposite to the equal sides of an isosceles triangle are equal and the sum of the measures of the three angles is 180°.
100° + x + x = 180°
2x = 180° – 100°
2x = 80°
x = \(\frac{80^{\circ}}{2}\) = 40°

(v) Base angles opposite to the equal sides of an isosceles triangles are equal and the sum of the measure of three angles of triangle is 180°.
x + x + 90° = 180°
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac{90^{\circ}}{2}\) = 45°

(vi) Base angles opposite to the equal sides of an isosceles triangle are equal and the sum of the measures of the three angles of triangle is 180°.
x + x + 40° = 180°
2x + 40° = 180°
2x = 180° – 40°
2x = 140°
x = \(\frac{140^{\circ}}{2}\)
= 70°
x = 70°

(vii) In the figure, two sides of the triangle are equal.
∴ The base angles opposite to equal sides are equal one of the base angle = x
other base angle = x
Now, x° and 120° form a linear pair = 180°
x + 120° = 180°
x = 180° -120°
= 60°
Thus, the value of x = 60°

(viii) In the figure, two sides of the triangle are equal.
since, one of the base angles = x
∴ The other base angle = x
Since, exterior angle is equal to sum of the interior opposite angles
∴ x + x = 110°
2x = 110°
x = \(\frac{110^{\circ}}{2}\) = 55°

(ix) Two sides of the triangle are equal.
∴ The base angles opposite to the equal sides are equal.
Since, one of the base angle = x
∴ The other base angle = x
Also, the vertically opposite angles 30° and x are equal.
∴ x = 30°

Question 2.
Find angles x and y in each figure.

Answer:
(i) Two sides of the triangle are equal.
∴ The base angles opposite to the equal sides are equal.
The other base angle is y.
Now y and 120° form a linear pair.
∴ y + 120° = 180°
y = 180° – 120° = 60°
∴ x + y + y = 180°
(sum of the three angles = 180°)
x + 60° + 60°= 180°
x+ 120° = 180°
x = 180° – 120°
= 60°
Thus x = 60° and y = 60°

(ii) Two sides of a triangles are equal.
∴ The base angles opposite to equal sides are equal. Since one of the base angle is ‘x’
∴ The other base angle = x
The given triangle is a right-angled triangle.
x + x + 90° = 180°
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac{90^{\circ}}{2}\) = 45°
Now x and y form a linear pair
x + y = 180°
45°+ y = 180°
y = 180° – 45° = 135°
Thus, x = 45° and y = 135°

(iii) In the given figure, two sides of a triangle are equal.
∴ The base angles are x and x
The third angle = 92°
(vertically opposite angles are equal)
x + x + 92° = 180°
(Sum of the three angles of a triangle is 180°)
2x + 92° = 180°
2x = 180° – 92°
2x = 88°
x = \(\frac{88^{\circ}}{2}\) = 44°
Now, x and y form a linear pair
x + y = 180°
44 + y = 180°
y = 180° – 44° = 136°
Thus, x = 44° and y = 136°

NCERT In-text Question Page No. 129 & 130
Question 1.
Find the unknown length x in the following figures.



(i) In the given right-angled triangle, the longest side (hypotenuse) is x
x² = 3² + 4²
(using pythagoras property)
= 9 + 16
= 25
or x² = 5²
x = \(\sqrt{25}\)
= 5
x = 5

(ii) The given figure is a right-angled triangle.
x² = 6² + 8²
(using pythagoras property)
= 36 + 64
x² = 100
x² = 10²
∴ x = 10

(iii) The given figure is a right-angled triangle.
x² = 8² + 15²
(using pythagoras property)
x² = 64 + 225
x² = 289
x² = 17²
x = 17

(iv) The given figure is a right-angled triangle
x² = 7² + 24²
(using pythagoras property)
x² = 49 + 576
x² = 625
x² = 25²
x = 25

(v) The given figure can be labelled as ΔABC and the altitude is AD. Consider the right-angled triangle ABD
AB² = AD² + BD²
(using pythagoras property)

37² = 12² + BD²
1369 = 144 + BD²
1369 – 144 = BD²
1225 = BD²
35² = BD²
∵ BD = 35
In the right-angled triangle ADC
AC² = AD² + DC²
(using pythagoras property)
37² = 12² + DC²
1369 = 144 +DC²
1369 – 144 = DC²
1225 = DC²
35² = DC²
∴ DC = 35
∵ BC = BD + DC
= 35 + 35
x = 70

(vi) In the given right-angled triangle
x² = 12² + 5²
(using the pythagoras property)
= 144 + 25
x² = 169
x² = 13²
∴ x = 13

These NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.2 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers Exercise 9.2

Question 1.
Find the sum:

Answer:

Question 2.

Answer:

|

Question 3.
(i) \(\frac{9}{2} \times\left(\frac{-7}{4}\right)\)
(ii) \(\frac{3}{10} \times(-9)\)
(iii) \(\frac{-6}{5} \times \frac{9}{11}\)
(iv) \(\frac{3}{7} \times\left(\frac{-2}{5}\right)\)
(v) \(\frac{3}{11} \times \frac{2}{5}\)
(vi) \(\frac{3}{-5} \times \frac{-5}{3}\)
Answer:

These NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.1 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers Exercise 9.1

Question 1.
List five rational numbers between
(i) -1 and 0
(ii) -2 and -1
(iii) \(\frac{-4}{5}\) and \(\frac{-2}{3}\)
(iv) \(\frac{-1}{2}\) and \(\frac{2}{3}\)
Answer:
(i) -1 and 0

(ii) -2 and -1

are the five rational numbers between -2 and -1

(iii) \(\frac{-4}{5}\) and \(\frac{-2}{3}\)

The five rational numbers are
\(\frac{-47}{60}<\frac{-23}{30}<\frac{-3}{4}<\frac{-11}{15} \text { and } \frac{-43}{60}\)

(iv) \(\frac{-1}{2}\) and \(\frac{2}{3}\)
L. C. M of 2 and 3 is 6

Question 2.
Write four more rational numbers in each of the following patterns.
(i) \(\frac{-3}{5}, \frac{-6}{10}, \frac{-9}{15}, \frac{-12}{20}\) ………………
(ii) \(\frac{-1}{4}, \frac{-2}{8}, \frac{-3}{12}\) ………………
(iii) \(\frac{-1}{6}, \frac{2}{-12}, \frac{3}{-18}, \frac{4}{-24}\) ………………
(iv) \(\frac{-2}{3}, \frac{2}{-3}, \frac{4}{-6}, \frac{6}{-9}\) ………………
Answer:

Thus, we observe a pattern in these numbers.
The next four more rational numbers are

The four required rational numbers are \(\frac{-15}{25}, \frac{-18}{30}, \frac{-21}{35}\) and \(\frac{-24}{40}\)

Thus, we observe a pattern in these numbers.
Next Four rational numbers are

The next four required rational numbers are \(\frac{-4}{16}, \frac{-5}{20}, \frac{-6}{24}\) and \(\frac{-7}{28}\)

Thus, we observe a pattern in these numbers
The next four rational numbers would be

The required four rational numbers are \(\frac{5}{-30}, \frac{6}{-36} ; \frac{7}{-42}\) and \(\frac{8}{-48}\)

Thus, we observe a pattern in these numbers
Four more rational numbers would be

The required four rational numbers are \(\frac{8}{-12}, \frac{10}{-15} ; \frac{12}{-18}\) and \(\frac{14}{-21}\)

Question 3.
Give four rational numbers equivalent to:
(i) \(\frac{-2}{7}\)
(ii) \(\frac{5}{-3}\)
(iii) \(\frac{4}{9}\)
Answer:
(i) Four rational numbers equivalent to

(ii) Four rational numbers equivalent to

(iii) Four rational numbers equivalent to

Question 4.
Draw the number line and represent the following rational numbers on it:
(i) \(\frac{3}{4}\)
(ii) \(\frac{-5}{8}\)
(iii) \(\frac{-7}{4}\)
(iv) \(\frac{7}{8}\)
Answer:

Question 5.
ThepointsP,Q,RS,T,U,AandBonthe number line are such that, TR = RS = SU
and AP = PQ = QB. Name the rational numbers represented by P, Q, R, and S.

Answer:
Since AP = PQ = QB
Distance between 2 and 3 is divided into 3 equal parts.
Similarly, distance between -2 and -1 is also divided into three equal parts.
P represents the rational number
\(\left(2+\frac{1}{3}\right) \text { i.e. } \frac{7}{3}\)
Q represents the rational number
\(\left(2+\frac{2}{3}\right) \text { i.e. } \frac{8}{3}\)
R represents the rational number
\(\left(-1-\frac{1}{3}\right) \text { i.e. } \frac{-4}{3}\)
S represents the rational number
\(\left(-1-\frac{2}{3}\right) \text { ie } \frac{-5}{3}\)

Question 6.
Which of the following pairs represent the same rational number?
(i) \(\frac{-7}{21}\) and \(\frac{3}{9}\)
(ii) \(\frac{-16}{20}\) and \(\frac{20}{-25}\)
(iii) \(\frac{-2}{-3}\) and \(\frac{2}{3}\)
(iv) \(\frac{-3}{5}\) and \(\frac{-12}{20}\)
(v) \(\frac{8}{-5}\) and \(\frac{-24}{15}\)
(vi) \(\frac{1}{3}\) and \(\frac{-1}{9}\)
(vii) \(\frac{-5}{-9}\) and \(\frac{5}{-9}\)
Answer:
(i) \(\frac{-7}{21}\) and \(\frac{3}{9}\)
Here \(\frac{-7}{21}\) is a negative rational number and \(\frac{3}{9}\) is a positive rational number.
\(\frac{-7}{21}=\frac{-1}{3} ; \frac{3}{9}=\frac{1}{3} ; \frac{-7}{21} \neq \frac{3}{9}\)
Thus, \(\frac{-7}{21}\) and \(\frac{3}{9}\) does not represent the same rational number.

(ii) \(\frac{-16}{20}\) and \(\frac{20}{-25}\)
We have \(\frac{-16}{20}\)= \(\frac{-4}{5}\)

Thus, \(\frac{-16}{20}\) and \(\frac{20}{-25}\) represent the same rational number.

(iii) \(\frac{-2}{-3}\) and \(\frac{2}{3}\)
\(\frac{-2}{-3}=\frac{+2}{3} ; \frac{2}{3}=\frac{2}{3}\)
Thus, \(\frac{-2}{-3}\) and \(\frac{2}{3}\) represent the same rational number.

(iv) \(\frac{-3}{5}\) and \(\frac{-12}{20}\)
We have, \(\frac{-3}{5}=\frac{-3}{5} ; \frac{-12}{20}=\frac{-3}{5}\)
So, \(\frac{-3}{5}=\frac{-12}{20}\)
Thus \(\frac{-3}{5}\) and \(\frac{-12}{20}\) represent the same rational number.

(v) \(\frac{8}{-5}\) and \(\frac{-24}{15}\)
We have, \(\frac{8}{-5}=\frac{-8}{5} ; \frac{-24}{15}=\frac{-8}{5}\)
So, \(\frac{8}{-5}\) = \(\frac{-24}{15}\)
Thus \(\frac{8}{-5}\) and \(\frac{-24}{15}\) represent the same rational number.

(vi) \(\frac{1}{3}\) and \(\frac{-1}{9}\)
Here \(\frac{1}{3}\) is positive integer and \(\frac{-1}{9}\) is a negative integer.
∴ \(\frac{1}{3} \neq \frac{-1}{9}\)
Thus \(\frac{1}{3}\) and \(\frac{-1}{9}\) does not represent the same rational number.

(vii) \(\frac{-5}{-9}\) and \(\frac{5}{-9}\)
\(\frac{-5}{-9}\) and \(\frac{5}{-9}\) is a positive integer.
and \(\frac{-5}{-9}\) = \(\frac{5}{-9}\) is a negative integer
∴ \(\frac{-5}{-9} \neq \frac{5}{-9}\)
Thus \(\frac{-5}{-9}\) and \(\frac{5}{-9}\) do not represent tha same rational number.

Question 7.
Rewrite the following rational numbers in the simplest form:
(i) \(\frac{-8}{6}\)
(ii) \(\frac{25}{45}\)
(iii) \(\frac{-44}{72}\)
(iv) \(\frac{-8}{10}\)
Answer:
(i) \(\frac{-8}{6}\)
\(\frac{-8}{6}=\frac{-4}{3}\) (Divide both sides by 2)
The simplest form is \(\frac{-4}{3}\)

(ii) \(\frac{25}{45}\)
\(\frac{25}{45}=\frac{5}{9}\) (Divide both sides by 5)
The simplest form is \(\frac{5}{9}\)

(iii) \(\frac{-44}{72}\)
\(\frac{-44}{72}=\frac{-11}{18}\)
Dividing both sides by 4)
The simplest \(\frac{-11}{18}\)

(iv) \(\frac{-8}{10}\)
\(\frac{-8}{10}=\frac{-4}{5}\) (Dividing both sides by 2)
The simplest form is \(\frac{-4}{5}\)

Question 8.
Fill in the boxes with the correct symbol out of > , <, and =


Answer:
\(\frac{-7}{6}\) is a negative rational number. 6

(ii) \(\frac{-4}{5} \text { and } \frac{-5}{7}\)
are negative rational numbers.
L.C.M of 5 and 7 is 35.

are negative rational numbers.
L.C.M of 8 and 16 is 16.

(iv) \(\frac{-8}{5}\) and \(\frac{-7}{4}\) are negative rational numbers.
LCM of 5 and 4 = 20

(v) \(\frac{1}{-3}\) and \(\frac{-1}{4}\) negative rational numbers.
L.C.M of 3 and 4 is 12.

(vi) \(\frac{5}{-11}\) and \(\frac{-5}{11}\) are negative rational numbers.

(vii) \(\frac{-7}{6}\) is a negative integer since 0 is 6
greater than every negative number.

Question 9.
Which is greater in each of the following?
(i) \(\frac{2}{3}, \frac{5}{2}\)
(ii) \(\frac{-5}{6}, \frac{-4}{3}\)
(iii) \(\frac{-3}{4}, \frac{2}{-3}\)
(iv) \(\frac{-1}{4}, \frac{1}{4}\)
(v) \(-3 \frac{2}{7} ;-3 \frac{4}{5}\)
Answer:
(i) \(\frac{2}{3}, \frac{5}{2}\)
L.C.M of 2 and 3 is 6

Thus \(\frac{5}{2}\) is greater rational number.

(ii) \(\frac{-5}{6}, \frac{-4}{3}\)
L.C.M of 6 and 3 is 6

Thus \(\frac{-5}{6}\) is greater rational number.

(iii) \(\frac{-3}{4}, \frac{2}{-3}\)
L.C.M of 4 and 3 is 12

\(\frac{2}{-3}>\frac{-3}{4}\)
Thus, the rational number \(\frac{2}{-3}\) is greater.

(iv) \(\frac{-1}{4}, \frac{1}{4}\)
since a positive rational number is always greater than a negative rational number.
\(\frac{1}{4}>\frac{-1}{4}\)
Thus, greater rational number is \(\frac{1}{4}\)

(v) \(-3 \frac{2}{7} ;-3 \frac{4}{5}\)

Thus, rational number -3\(\frac{2}{7}\) is greater.

Question 10.
Write the following rational numbers in ascending order.
(i) \(\frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5}\)
(ii) \(\frac{-1}{3}, \frac{-2}{9}, \frac{-4}{3}\)
(iii) \(\frac{-3}{7}, \frac{-3}{2}, \frac{-3}{4}\)
Answer:
(i) \(\frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5}\)
\(-\frac{3}{5}<-\frac{2}{5}<-\frac{1}{5}\)
The ascending order is \(-\frac{3}{5},-\frac{2}{5},-\frac{1}{5}\)

(ii) \(\frac{-1}{3}, \frac{-2}{9}, \frac{-4}{3}\)
L.C.M of 3 and 9 is 9

Thus, the ascending order is
\(\frac{-4}{3}, \frac{-1}{3}, \frac{-2}{9}\)

(iii) \(\frac{-3}{7}, \frac{-3}{2}, \frac{-3}{4}\)
L.C.M of 7, 2 and 4 is 28

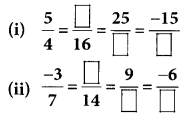
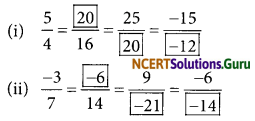
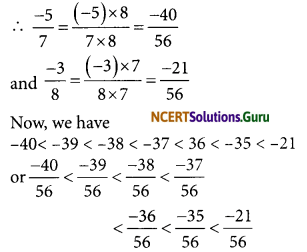
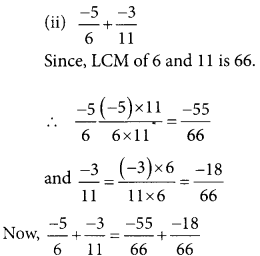
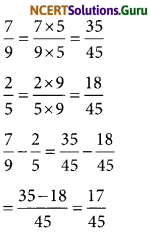
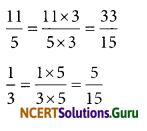
These NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.5 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties Exercise 6.5

Question 1.
PQR is a triangle, right-angled at P. If PQ = 10 cm and PR = 24 cm, find QR. Ans: In the right APQR
Answer:
In the right ΔPQR

QR² = PQ² + PR²
(pythagoras property)
= 10² + 24²
= 100 + 576
= 676
QR² = 26²
∴ QR = 26 cm

Question 2.
ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Answer:
In the right ΔABC

AB² = AC² + BC²
(using pythagoras property)
25² = 7² + BC²
625 = 49 + BC²
625 – 49 = BC²
576 = BC²
24² = BC²
∴ BC = 24 cm

Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
Answer:
Let the distance of the foot of a ladder from the wall be ‘a’m

a2² + 12² = 15²
(using pythagoras property)
a² + 144 = 225
a² = 225 – 144
a² = 81
a² = 9²
a = 9 m
The distance of the foot of the ladder from the wall = 9 m.

Question 4.
Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Answer:
(i) 2.5 cm, 6.5 cm, 6 cm².
The longest side is 6.5 cm
2.5² + 6² = 6.25 + 36
= 42.25
6.5² = 42.25
∴ 6.5² = 2.5² + 6²
(pythagoras property)
The given lengths can be the sides of a right triangle.
The right angle is the angle between the sides 2.5 cm and 6 cm

(ii) 2 cm, 2 cm, 5 cm
The longest side is 5 cm
2² + 2² = 4 + 4 = 8
5² = 25
5² ≠ 2² + 2²
∴ The given length cannot be the sides of a right triangle.

(iii) 1.5 cm, 2 cm, 2.5 cm
The longest side is 2.5 cm
1.5² + 2² = 2.25 + 4
= 6.25
2.5² = 6.25
1.5² + 2² = 2.5²
(pythagoras property)
The given lengths can be sides of a right triangle.
The right angle is the angle between the sides 1.5 cm and 2 cm.

Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.

Answer:
Let the tree BD be broken at the point C, such that CD = CA
In the right triangle ABC, using the pythagoras property; we get
AC² = AB² + BC²
AC² = 12² + 5²
= 144 + 25
AC² = 169
AC² = 13²
∴ AC = 13
Now, height of the tree
BD = BC + CD (CD = AC)
= 5 m + 13 m
= 18 m
The height of the tree is 18 m.

Question 6.
Angles Q and R of PQR are 25° and 65°. Write which of the following is true:
(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²
Answer:
In ΔPQR
∠P + ∠Q +∠R = 180°
∠P + 25° + 65° = 180°

∠P + 90° = 180°
∠P = 180° – 90°
= 90°
So, ΔPQR is a triangle right angled at P.
∴ QR is the hypotenuse.
∴ using the pythagoras property
QR² = PQ² + PR² So,

(ii) PQ² + RP² = QR² is true

Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Answer:
Let the breadth AD be x cm.
In the right triangle ABD,

BD² = AD² + AB²
41²= x² + 40²
x² = 41² – 40²
= 1681 – 1600
x² = 81
x² = 9²
x = 9 cm
Perimeter of the rectangle = 2 (l + b)
= 2 (40 + 9)
= 2 × 49
= 98 cm
Thus, the perimeter of the rectangle
= 98 cm

Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Answer:
Since the diagonals of a rhombus bisect each other at right angles.

∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
AO = \(\frac { 1 }{ 2 }\) AC; AO = \(\frac { 1 }{ 2 }\) × 30 = 15
∵ AO = OC = 15 cm and BO = OD = 8 cm
In the right ΔAOB,
AB² = AO² + BO²
AB² = 15² + 8²
AB² = 225 + 64
AB² = 289
AB² = 17²
AB = 17 cm
∵ Side of the rhombus is 17 cm.
∴ Perimeter of the rhombus ABCD = 4 × 17
(all the four sides are equal) = 68 cm