CBSE Class 9

These NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.2 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Exercise 9.2

Question 1.
In fig. 9.15, ABCD is a parallelogram and AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm. Find AD.

Solution:
In this fig. we have given AB = 16 cm, AE = 8 cm, CF = 10 cm and ABCD is a parallelogram.
∴ AB = CD (opp side of parallelogram)
∴ CD = 16 cm
Again we know that,
Area of parallelogram = Base × Corresponding altitude
∴ Area of parallelogram ABCD = CD × AE
= 16 × 8
= 128 cm² …..(i)
Again Area of parallelogram = AD × CF
128 = AD × 10 (from equ. (i))
AD = \(\frac{128}{10}\) = 12.8 cm
AD = 12.8 cm

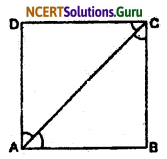
Question 2.
If E, F, G and H are respectively the mid points of the sides of a parallelogram ABCD. show that ar(EFGH) = \(\frac {1}{2}\) ar(ABCD).
Solution:
Given: ABCD is a parallelogram, in which E, F, G, and H are the midpoints of sides AB, BC, CD, and AD respectively.

To prove that
ar(||gm EFGH) = \(\frac {1}{2}\) ar (||gm ABCD)
Construction: Join HF
Proof: ABCD is a ||gm
∴ AD || BC and AD = BC
∴ AH = BF and AH || BF
Therefore, ABFH is a ||gm.
Since, ∆HEF and || gm HABF are on the same base HF and between the same parallel lines, AB and HF
∴ ar(∆HEF) = \(\frac {1}{2}\) ar(||gm HABF) …….(i)
Similarly, ∆HGF and ||gm HDCF are on same base HF and between the same parallel lines, DC and HF.
∴ ar (∆HGF) = \(\frac {1}{2}\) ar (|| gm HDCF) …….(ii)
Adding (i) and (ii) we get
ar(∆HEF) + ar(∆HGF)
= \(\frac {1}{2}\) ar(|| gm HABF) + \(\frac {1}{2}\) ar(||gm HDCF) + ar (|| gm FFGH)
= \(\frac {1}{2}\) [ar(||gm HABF) + ar (||gm HDCF)]
or, ar (||gm EFGH) = \(\frac {1}{2}\) ar (|| gm ABCD)

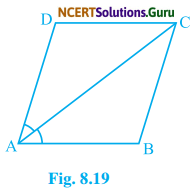
Question 3.
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD shows that ar(∆APB) = ar(∆BQC).
Solution:
Given: ABCD is a || gm in which P and Q are the points on side DC and AD respectively.
To prove that: ar(∆APB) = ar(∆BQC)
Proof: ABQC and || gm ABCD lie on the same base BC and between the same parallel lines.

∴ ar (∆BQC) = \(\frac {1}{2}\) ar(||gm ABCD) ……(i)
Similarly, ∆APB and ||gm ABCD lie on the same base AB and between same parallel lines.
∴ ar(∆APB) = \(\frac {1}{2}\) ar (||gm ABCD) ……(ii)
From equation (i) and (ii), we can say
ar(∆BQC) = ar(∆APB)

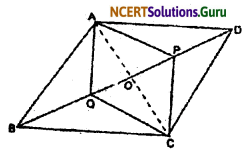
Question 4.
In fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(∆APB) + ar(∆PCD) = \(\frac {1}{2}\) ar (||gm ABCD)
(ii) ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)

Solution:
Given: ABCD is a || gm in which P is any point interior to it.
To prove that:
(i) ar(∆APB) + ar(∆PCD) = \(\frac {1}{2}\) ar (||gm ABCD)
(ii) ar (∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)

Construction: Through P draw a line parallel to AB which interacts with AD at M and BC at N.
Proof: In parallelogram ABCD,
AB || CD (opp sides of a ||gm)
But, AB || MN (by construction)
∴ MM || CD
In ABNM
AB || MN and AM || BN (opp sides of || gm)
∴ ABNM is a || gm
Again, ∆APB and || ABNM lie on the same base AB and between the same parallel lines AB and MN.
∴ ar (∆APB) = \(\frac {1}{2}\) ar (|| gm ABNM) ……(i)
Similarly, MNCD is a parallelogram.
Since ∆PCD and || gm MNCD lie on same base CD and between same parallel lines CD and MN.
Therefore, ar (∆PCD) = \(\frac {1}{2}\) ar (|| gm MNCD) ……(ii)
Adding (i) and (ii) we get,
ar(∆APB) + ar(∆PCD) = \(\frac {1}{2}\) [ar (|| gm ABNM) + ar (|| gm MNCD)]
∴ ar(∆APB) + ar(∆PCD) = \(\frac {1}{2}\) [ar (|| gm ABCD) ……(iii)

(ii) Similarly, itive draw a line through P and parallel to D.
Then, ar(∆APD) + ar(∆PBC) = \(\frac {1}{2}\) ar (|| gm ABCD) ……(iv)
From equation (iii) and (iv) we can say
ar(∆APP) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)

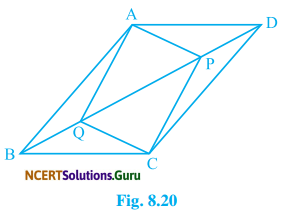
Question 5.
In fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (|| gm PQRS) = ar (|| gm ABRS)
(ii) ar (∆AXS) = \(\frac {1}{2}\) ar (|| gm PQRS)

Solution:
Parallelograms PQRS and ABRS are lying on the same base SR and in between the same parallel lines SR and PB.

We know that parallelograms lie on the same base and between the same parallel lines are equal in area,
∴ ar(|| gm PQRS) = ar(|| gm ABRS) ……(i)

(ii) Again, ∆AXS and || gm ABRS lie on the same base AS and between the same parallel lines AS and BR.
∴ ar (∆AXS) = \(\frac {1}{2}\) ar (|| gm ABRS)
or, ar (∆AXS) = \(\frac {1}{2}\) ar (|| gm PQRS) (from equ. (i))

Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to point P and Q. In how many parts the field is divided? What is the shape of these parts? The fanner wants to saw wheat and pulses in equal portions of the field separately. How should she do it?
Solution:
According to the question, fields is divided into three-part. The shape of the three parts is triangular as ∆PSA, ∆PAQ, and ∆QRA.

Again, according to the question, the farmer wants to sow wheat and pulses in an equal portion of the field separately.
We know that if a parallelogram and triangle are on the same base and between the same parallels, then the area of the triangle is half the area of the parallelogram.
∴ ar(∆PAQ) = \(\frac {1}{2}\) ar (|| gm PQRS)
or, ar(∆PAQ) = ar(∆PSA) + ar(∆QRA)
So, farmers must sow wheat in triangular parts PAQ and pluses in other two triangular parts PSA and QRA, or, pulses in triangular parts PAQ and wheat in other two triangular parts PSA and QRA.

These NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.1 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Exercise 9.1

Question 1.
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

Solution:
(i) In figure 9.8(i), trapezium ABCD and triangle PCD have a common base CD and between seine parallels AB and CD.

(ii) In fig 9.8 (ii), parallelogram PQRS and trapezium MNRS have common base RS, but they are not in the same parallels.

(iii) In figure 9.8(iii), parallelogram PQRS and triangle TQR have a common base QR and between same parallels QR and PS.

(iv) In figure 9.8(iv), parallelogram ABCD and triangle PQR have no common base but they are in between the same parallels AD and BC.

(v) In figure 9.8(v), parallelogram ABCD and parallelogram APQD have a common base AD, and between same parallels AD and BQ.

(vi) In figure 9.8(vi), parallelograms PBCS and PBAD lie on the same base PS, but not in the same parallels.

These NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Ex 8.2 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.2

Question 1.
ABCD is a quadrilateral in which P, Q, R, and S are midpoints of the sides AB, BC, CD, and DA (see fig. 8.29). AC is a diagonal. Show that
(i) SR || AC and SR = \(\frac {1}{2}\) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

Solution:
Given. ABCD is a quadrilateral in which P, Q, R, and S are the midpoints of side AB, BC, CD, and AD respectively.
To prove that:
(i) SR || AC and SR = \(\frac {1}{2}\) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
Proof:
(i) In ΔADC
S and R are the mid-point of side AD and DC respectively.
We know that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is half of it.
SR || AC and SR = \(\frac {1}{2}\) AC ……(i)

(ii) In ΔABC,
P and Q are the mid points of side AB and BC respectively.
Therefore, PQ || AC and PQ = \(\frac {1}{2}\) AC …….(ii)
From equation (i) and (ii),
PQ || SR and PQ = SR

(iii) We have
PQ = SR (Prove above)
and PQ || SR (Prove above)
We know that if one pair of opposite sides of a quadrilateral are parallel and equal then the quadrilateral is a parallelogram.
∴ PQRS is parallelogram.

Question 2.
ABCD is a rhombus and P, Q, R, and S are the midpoints of the sides AB, BC, CD, and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
Given: Arhmbus ABCD in which P, Q, Rand S are the midpoints of sides AB, BC, CD, and DA respectively. PQ, QR, RS, and SP are joined.
To prove that: PQRS is a rectangle.
Construction: Join AC and BD.

Proof: In order to prove that PQRS is a rectangle, it is sufficient to show that it is a parallelogram whose one angle is a right angle. First, we shall prove that PQRS is a parallelogram.
In ΔABC,
P and Q are the mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac {1}{2}\) AC ……(i)
In ΔADC,
R and S are the mid points of CD and AD respectively.
∴ RS || AC and RS = \(\frac {1}{2}\) AC ……(ii)
From equation (i) and (ii) we have
PQ || RS and PQ = RS
Thus, PQRS is a quadrilateral such that one pair of opposite sides PQ and SR is equal and parallel. So, PQRS is a parallelogram.
PQ || AC (Opposite sides of || gm)
∴ MQ || ON
QR || BD (Opposite sides of || gm)
∴ QN || OM
Therefore, OMQN is a parallelgram.
and ∠NOM = 90°
[Diagomals of a rhombus bisects each other at a right angle]
So, ∠MQN = 90°
[Opposite angles of || gm are equal]
Therefore, PQRS is a parallelogram in which ∠Q is a right angle.
∴ PQRS is a rectangle.

Question 3.
ABCD is a rectangle and P, Q, R, and S are midpoints of the sides AB, BC, CD, and DA respectively. Show that the quadrilateral PQRS is a rhombus.

Solution:
Given: A rectangle ABCD in which P, Q, R, and S are the midpoints of sides AB, BC, CD, and DA respectively. PQ, QR, RS, and SP are joined.
To prove that: PQRS is a rhombus.
Construction: Join AC and BD.
Proof: In ∆ABC,
P and Q are mid points of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac {1}{2}\) AC …..(i)
Similarly in ∆ACD,
SR || AC and SR = \(\frac {1}{2}\) AC ……(ii)
From equation (i) and (ii) we have
PQ || SR and PQ = SR
Therefore, PQRS is a parallelogram
∴ SR || PQ (Opposite sides of || gm PQRS)
and SR = PQ
Now, in ∆BCD,
Q and R are mid points of side BC & CD.
∴ QR || AC and QR = \(\frac {1}{2}\) BD
But, AC = BD (In rectangle diagonals are equal)
QR = \(\frac {1}{2}\) AC ……(iii)
From equation (i) and (iii) we have
PQ = QR
but PQ = SR and PS = QR
Therefore, PQ = QR = RS = PS
∴ PQRS is a rhombus.

Question 4.
ABCD is a trapezium in which AB || DC, BD is a diagonal, and E is the midpoint of AD. A line is drawn through E parallel to AB intersecting BC at F (see fig. 8.30). Show that F is the midpoint of BC.

Solution:
In ∆ABD,
E is the midpoints of AD and EF || AB
∴ EF || CD
We know that a line through the midpoint of a side of a triangle parallel to another side bisects the third side. So, G is the midpoint of DB.
Now, in ∆DBC
G is the midpoint of DB and GF || CD
∴ F is the midpoint of BC.

Question 5.
In a parallelogram ABCD, E and F are the midpoints of sides AB and CD respectively (see fig. 8.31). Show that the line segment AF and EC trisect the diagonal BD.

Solution:
We have,
ABCD is a parallelogram
∴ AB || CD
So, AE || FC ……(i)
Again, AB = CD (Opposite sides of ||gm ABCD)
∴ \(\frac {1}{2}\) AB = \(\frac {1}{2}\) CD
or, AE = FC …….(ii)
From equation (i) and (ii)
Therefore, AFCE is a parallelogram.
Now, in ΔDQC,
F is the mid point of CD,
and FP || CQ
We know that a line through the midpoint of a side of a triangle parallel to another side bisects the third side.
So, P is the midpoint of DQ
or, DP = PQ ……(i)
Similarly in ΔAPB, Q is midpoint of BP
i.e. PQ = BQ …..(ii)
From equation (i) and (ii)
PQ = DP = BQ
∴ AF and CE trisect the diagonal BD.

Question 6.
Show that the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.
Solution:
Given: ABCD is a quadrilateral in which P, Q, R, and S are the midpoints of side AB, BC, CD, and AD respectively.
To prove that: PR & QS bisect each other. Construction: Join PQ, QR, RS, and SP and join BD.
Proof: In ΔABD,
S and P are the midpoint of side AD and AB respectively we know that the line segment joining the midpoints of any two sides of a triangle is. parallel to the third side and is half of it.

Therefore, SP || BD and SP = \(\frac {1}{2}\) BD …….(i)
Similarly,
In ΔBCD,
Q and R is the mid points of side BC & CD
∴ QR || AC and QR = \(\frac {1}{2}\) AC ……(ii)
From equation (i) and (ii)
SP || QR and SP = QR
We know that if one opposite pair of a quadrilateral are parallel and equal, then the quadrilateral is a parallelogram.
∴ SPQR is a parallelogram.
So, PR and QS bisect each other.
[Because diagonal of a parallelogram bisects each other]

Question 7.
ABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid point of AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac {1}{2}\) AB
Solution:
Given: ABC is a right-angled triangle right angle at C. M is the midpoint of side AB and DM || BC.
To prove that:
(i) D is the mid point of AC
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac {1}{2}\) AB

Construction: Join CM.
Proof: (i) In ΔABC,
M is the mid point of side AB and MD || BC
We know that a line through the midpoint of a side of a triangle parallel to another side bisects the third side.
So, D is the midpoint of AC.

(ii) We have DM || CB
∴ ∠MDC + ∠DCB = 180°
(Sum of interior angles of the same side of transveralsi)
or, ∠MDC + 90° = 180°
or, ∠MDC = 90°
Therefore, MD ⊥ AC

(iii) In ΔAMD and ΔCMD
AD = CD (Prove above)
∠ADM = ∠CDM, (Each 90°)
DM = DM (Common)
By S-A-S congruency condition
ΔAMD ≅ ΔCMD
∴ AM = CM …..(i) (By CPCT)
But AM = AB ……(ii)
(Given M is the mid point of AB)
From (i) and (ii)
CM = MA = \(\frac {1}{2}\) AB

These NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Ex 8.1 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1

Question 1.
The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. the angles of the quadrilateral.
Solution:
Let the first angle of the quadrilateral be 3x.
Second angle of quadrilateral is 5x.
The third angle of the quadrilateral is 9x.
The fourth angle of the quadrilateral is 13x.
Therefore,
3x + 5x + 9x + 13x = 360 (sum of all four angles of a quadrilateral is 360)
⇒ 30x = 360
⇒ x = \(\frac{360}{30}\)
⇒ x = 12
First angle of quadrilateral is 3x = 3 × 12 = 36°
Second angle of quadrilateral is 5x = 5 × 12 = 60°
Third angle of quadrilateral is 9x = 9 × 12 = 108°
Fourth angle of quadrilateral is 13x = 13 × 12 = 156°

Question 2.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Given: ABCD is a parallelogram, in which diagonal AC and BD are equal.
To prove that: ABCD is a rectangle.

Proof: In ∆ABC and ∆DCB.
AC = BD (Given)
BC = GB (Common)
AB = DC (Opposite sides of a parallelogram)
Therefore, by S-S-S congruency condition
∆ABC ≅ ∆DCB
So, ∠ABC = ∠BCD (By C.P.C.T)
But, ∠ABC + ∠BCD = 180 (Sum of interior angles of the same side of transversal)
⇒ 2∠ABC = 180 (∵ ∠ABC = ∠BCD)
⇒ ∠ABC = 90°
Therefore, paraileiogram ABCD is a rectangle.

Question 3.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
Given: ABCD is a quadrilateral, in which diagonal AC and BD intersect each other at a right angle.
To prove that ABCD is a Rhombus.
Proof: In ∆AOD and ∆AOB,
AO = OA (Common)
OD = OB (Given)
∠AOD = ∠AOB (each 90°)
By S-A-S congruency condition
∠AOU ≅ ∠AQB
So, AD = AB …..(i) (By C.P.C.T)
Similarly, AD = BC ……(ii)
and AB = CD ……(iii)
By equation (i), (ii) and (iii)
AB = BC = CD = DA
Therefore, ABCD is a rhombus.

Question 4.
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
Given: ABCD is a square, in which diagonal AC and BD intersect each other at Q.

To prove that:
(i) AC = BD
(ii) Diagonal bisects each other at right angle.
Proof:
(i) In ∆ABC and ∆BAD
AB = BA (Common)
BC = AD (sides of square)
∠ABC = ∠BAD (each 90°)
By S-A-S congruency condition
∆ABC ≅ ∆BAD
AC = BD (By C.P.C.T.)

(ii) In ∆AOB and ∆COD,
AB = CD (Sides of square)
∠AOB = ∠COD (Vertically opposite angles)
∠OBA = ∠OCD (Alternate interior angle)
Therefore, by A-S-A congruency condition
∆AOB ≅ ∆COD
So, OA = OC (By C.P.C.T.)
and OB = OD (By C.P.C.T)
Now, In ∆AOD and ∆COD
AD = CD (Sides of square)
OA = OC (Prove above)
OD = OD (Common)
By S-S-S ccngruency condition
∆AOD = ∆COD
So, ∠AOD = ∠COD (By C.P.C.T)
But, ∠AOD + ∠COD = 180 (Linear pair)
⇒ ∠AOD + ∠AOD = 180 (∵ ∠AOD = ∠COD)
⇒ 2∠AOD = 180
⇒ ∠AOD = 90° …..(ii)
Therefore, from equations (i) and (ii) it is dear that diagonal of a square bisect each other at a right angle.

Question 5.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
Given: ABCD is a quadrilateral in which diagonal AC and BD bisect each other at right angles.

To prove that: ABCD is a square.
Proof: In ∆AOB and ∆COD
AO = CO (Given)
∠AOB = ∠COD (Vertically opposite angles)
OB = OD (Given)
By S-A-S Congruency Condition.
∆AOB ≅ ∆COD
So, AB = CD …..(i) (By C.P.C.T)
and ∠OAB = ∠OCD (By C.P.C.T)
But it is the pair of alternate interior angles and we know that if pair of alternate interior angles are equal then the two lines are parallel.
∴ AB || CD …..(ii)
From (i) and (ii)
ABCD is a parallelogram
Now, in ∆AOD and ∆COD
AO = OC (Given)
∠AOD = ∠COD (Each 90°)
OD = OD (Common)
By S-A-S congruency condition
∆AOD ≅ ∆COD
AD = CD …..(iii) (ByC.P.C.T.)
Again, AD = BC ……(iv)
(Opposite sides of parallel gram ABCD)
From equation (i), (iii) and (iv)
Therefore ABCD is a square.

Question 6.
Diagonal AC of a parallelogram ABCD bisects ∠A [see Fig. 8.19]. Show that
(i) it bisects ∠C also.
(ii) ABCD is a rhombus.

Solution:
(i) In ∆DAC and ∆BCA
DA = BC (Opposite sides of parallelogram)
DC = BA (Opposite sides of parallelogram)
AC = CA (Common)
By S-S-S congruency condition
∆DAC = ∆BCA
So, ∠DAC = ∠BCA …..(i) (By C.P.C.T)
and ∠ACD = ∠BAC ……(ii) (By C.P.C.T)
Add equation (i) and (ii)
∠DAC + ∠ACD = ∠BCA + ∠BAC
∠DAC + ∠ACD = ∠BCA + ∠DAC (∵ ∠DAC = ∠BAC given)
Therefore, ∠ACD = ∠BCA
or, AC bisect ∠C.

(ii) We have,
∠ACD = ∠BAC …..(iii) (From equation (ii))
But ∠BAC = ∠CAD …..(iv)
From (iii) and (iv)
∠ACD = ∠CAD
∴ DA = DC
(Side opposite to equal angles are equal)
But DA = BC (Opposite side of || gm)
∴ AB = BC = CD = DA
Therefore, ABCD is a rhombus.

Question 7.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Solution:
In this Fig. ABCD is a rhombus.

Therefore, AB = BC = CD = AD
In ∆ABC,
AB = BC (Because ABCD is a rhombus)
∴ ∠1 = ∠2 (Angle opposite to equal sides are equal)
But, ∠1 = ∠3 …….(ii) (Alternate interior angles)
From (i) and (ii)
∠1 = ∠3
∴ AC bisects ∠C.
Similarly, we can prove AC bisects ∠A, and BD bisects both ∠B as well as ∠D.

Question 8.
ABCD is a rectangle in which diagonal AC bisects. ∠A as well as ∠C. Show that
(i) ABCD is a square.
(ii) diagonal BD bisects ∠B as well as ∠D.

Solution:
(i) We have given ABCD is a rectangle.
∠A = ∠C (each 90°)
or, \(\frac {1}{2}\) ∠A = \(\frac {1}{2}\) ∠C
∠DAC = ∠DCA (AC bisects ∠A as well as ∠C)
So, AD = CD ……(i) (Sides opposite to equal angles are equal)
But, AD = BC ……(ii) (Opposite sides of rectangle)
From equation (i) and (ii)
AB = BC = CD = AD
∴ ABCD is rhombus.
But, each angle of rhombus ABCD is 90°.
Therefore, ABCD is a square.

(ii) We know that diagonals of squares bisect opposite angles.
Therefore, diagonal BD bisects both ∠B and ∠D.

Question 9.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig 8.20) Show that:
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB = ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

Solution:
Given: ABCD is a parallelogram, and two points P and Q are taken on diagonal BD such that DP = BQ.
To prove that:
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB = ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.

Construction: Draw diagonal AC of parallelogram ABCD intersecting BD at O.
Proof:
(i) In ∆APD and ∆CQB
∠ADP = ∠CBQ (Pair of alternate interior angles)
AD = BC (Opposite sides of || gm ABCD)
PD = QB (Given)
By S-A-S congruency condition.
∠APD ≅ ∠CQB

(ii) We have
∠APD ≅ ∠CQB (Prove above)
∴ AP = CQ (By C.P.C.T.)

(iii) In ∆AQB and ∆CPD
∠LBQ = ∠CDP (Pair of alternate interior angles)
AB = CD (Opposite sides of parallelogram ABCD)
BQ = DP (Given)
By S-A-S congruency condition
∆AQB ≅ ∆CPD

(iv) We have
∆AQB ≅ ∆CPD (Prove above)
∴ AQ = CP (By C.P.C.T)

(v) In ∆QCP,
AQ = CP (Prove above from (iv))
and AP = CQ (Prove above from (ii))
We know that if both opposite pairs are equal then the parallelogram.
Hence, APCQ is a parallelogram.

Question 10.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A arid C on diagonal BD respectively (see fig 8.21). Show that
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ

Solution:
(i) In ∆APB and ∆CQD
∠APB = ∠CQD (Each 90°)
AB = CD (Opposite sides of || gm ABCD)
and, ∠ABP = ∠CDQ (Alternate interior angles)
By A-S-A Congruency condition
∆APB = ∆CQD

(ii) We have
∆APB = ∆CQD (Prove above)
∴ AP = CQ (By C.P.C.T)

Question 11.
In ∆ABC and ∆DEF, AB = DE and AB || DE, BC = EF and BC || EF. Vertices A, B, and C are joined to vertices D, E and F respectively (see fig 8.22). Show that
(i) quadrilateral ABED is a parallelogram.
(ii) quadrilateral BEFC is a parallelogram.
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF

Solution:
Given: AB = DE and AB || DE,
BC = EF and BC || EF
To prove that:
(i) quadrilateral ABED is a parallelogram.
(ii) quadrilateral BEFC is a parallelogram.
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
Proof:
(i) We have
AB = DE and AB || DE
We know that if one opposite pair of a quadrilateral are parallel and equal, then the quadrilateral is a parallelogram.
∴ Quadrilateral ABDE is a parallelogram.

(ii) We have
BC = EF and BC || EF
Therefore, quadrilateral BCEF is a parallelogram.

(iii) From (i) we have
ABED is a parallelogram.
AD = BE and AD || BE …….(A)
(Opposite sides of parallelogram ABED)
Again, From (ii)
BEFC is a parallelogram,
BE = CF and BE || CF ……..(B)
(Opposite sides of parallelogram BEFC)
From equation (A) and (B)
AD || CF and AD = CF

(iv) We have
AD || CF and AD = CF (Prove above from part (iii))
We know that, if one opposite pair of a quadrilateral are parallel and equal, then the quadrilateral is a parallelogram.
∴ ACFD is a parallelogram.

(v) We have,
ACFD is a parallelogram
(Prove above from part IV)
∴ AC || DF
(Opposite sides of parallelogram ACFD)
and AC = DF

(vi) In ∆ABC and ∆DEF
AB = DE (Given)
BC = EF (Given)
AC = DF (Prove above)
By S-S-S Congruency condition,
∆ABC ≅ ∆DEF.

Question 12.
ABCD is, a trapezium in which AB || CD and AD = BC (see fig 8.23). Show that
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) Diagonal AC = Diagonal BD.

Solution:
Given: ABCD is a trapezium in which AB || CD and AD = BC.
To prove that:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) Diagonal AC = diagonal BD.
Construction: Through C draw CE || AD which intersect AB produced at E, and join ACBD.

Proof: (i) We have,
AB || CD (Given)
AD || CE (By construction)
Therefore, AECD is a parallelogram.
So, AD = CE …..(i)
(Opposite sides of || gm)
But AD = BC ……(ii) (Given)
From (i) and (ii)
BC = CE
∴ ∠CBE = ∠CEB
(Angle opposite to equal sides are equal)
Now, ∠A + ∠CEB = 180°
(Sum of interior angles of the same side of transversal)
or, ∠A + ∠CBE = 180° ……(iii) (∵ ∠CEB = ∠CBE)
But, ∠B + ∠CBE = 180° ……(iv) (Linear pair)
From equation (iii) and (iv)
or, ∠A = ∠B

(ii) We have AB || CD
∴ ∠A + ∠D = 180° …..(v)
(Sum of an interior angle of the same side of transversal)
and, ∠C + ∠B = 180° ……(vi)
(Sum of interior angle of the same side of transversal)
From equation (v) and (vi)
∠A + ∠D = ∠C + ∠B
But, ∠A = ∠B (Prove above)
∴ ∠C = ∠D

(iii) In ∆ABC and ∆BAD
AB = BA (Common)
BC = AD (Given)
∠B = ∠A (Prove above)
By S-A-S congruency condition
∆ABC ≅ ∆BAD

(iv) We have
∆ABC ≅ ∆BAD (Prove above)
∴ AC = BD (By CPCT)
Therefore, diagonal AC = diagonal BD.

These NCERT Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.5 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 7 Triangles Exercise 7.5

Question 1.
ABC is a triangle. Locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABC.
Solution:
To locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABC, we take the following steps:

Step I: Draw any triangle ABC.
Step II: Draw perpendicular bisector of side BC and AB.
Step III: Both bisectors intersect each other at point P.
Therefore, P is a point interior of ∆ABC which is equidistant from all the vertices of ∆ABC.

Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Solution:
To locate a point in the interior of the triangle which is equidistant from all the sides of the triangle, we take the following steps:

Step I: Draw any triangle ABC.
Step II: Draw angle bisector of ∠B and ∠C.
Step III: Both angle bisectors intersects each other at P.
Therefore, P is the point at which all three sides of ∆ABC are equidistant.

Question 3.
In a huge park, people are concentrated at three points (see Fig. 7.52).

A: Where there are different slides and swings for children.
B: Near which a man-made lake is situated.
C: Which is near to a large parking and exit.
Where should an ice cream parlour be set up so that the maximum number of people can approach it?
Solution:
An ice cream parlour should be set at a point in which A, B, and C are equidistant.
For this we can take the following steps:

Step I: Join A to B, B to C, and C to A.
Step II: Draw perpendicular bisector of BC and AB.
Step III: Both perpendicular bisectors intersect each other at P.
Therefore, P is the required point, in which ice cream parlour should be set up so that the maximum number of people can approach it.

Question 4.
Complete the hexagonal and star-shaped Rangolies [see Fig. 7.53 (i) and (ii)] by filling them as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

Solution:
Fig. 5.53 (ii) has more equilateral triangles of side 1 cm. As Fig. 7.53 (i) is inside Fig. 7 53 (ii). It is because the area of star-shaped Rangolies is greater than that of hexagonal Rangoli.

These NCERT Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.4 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 9 Maths Chapter 7 Triangles Exercise 7.4

Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.
Solution:

In right angled triangle ABC
∠A + ∠B + ∠C = 180° (Angle sum property of A)
or, ∠A + ∠C + 90 = 180° (∵ ∠B = 90)
or, ∠A + ∠C = 90°
∴ ∠B > ∠A
Therefore, AC > BC …….(i)
(Side opposite to greater angle is greater)
Again, ∠B > ∠C
∴ AC > AB ……(ii)
(Side opposite to greater angle is greater larger)
From equation (i) and (ii)
AC is longer then both AB and BC.
Therefore AC is longes side of ∆ABC.

Question 2.
In Fig. 7.48 side AB and AC of ∆ABC are extended to point P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

Solution:
In ∆ABC, we have given,
∠PBC < ∠QCB ……(i)
Now, ∠PBC + ∠ABC = 180° …..(ii) (Linear pair)
Again, ∠QCB + ∠ACB = 180° ……(iii) (Linear pair)
From equation (ii) and (iii)
∠PBC + ∠ABC = ∠QCB + ∠ACB
But ∠PBC < ∠QBC Therefore, ∠ABC > ∠ACB
∴ AC > AB (Side opposite to greater angle is greater)

Question 3.
In Fig. 7.49, ∠B > ∠A and ∠C < ∠D. Show thatn AD < BC.

Solution:
In ∆BAO,
∠B < ∠A
∴ OA < OB ……(i)
(Single opposite to greater angle is greater)
Again, In ∆CDO
∠C < ∠D
∴ OD < OC ……(ii)
(Single opposite to greater angle is greater)
Add equation (i) and (ii)
OA + OD < OB + OC
AD < BC

Question 4.
AB and CD are respectively the smallest and longest sides of quadrilateral ABCD (se Fig. 7.50). Show that ∠A > ∠C and ∠B > ∠D.

Solution:
Given ABCD is a quadrilateral in which AB is smallest and CD is longest side.
To prove that:
(i) ∠A > ∠C
(ii) ∠B > ∠D
Construction: Join A and C.
Proof: In ∆ABC
AB < BC (∵ AB is smallest side)
∴ ∠BCA < ∠BAC …..(i)
(∵ Angle opposite to larger side is greater)
Again, In ∆ACD,
AD < CD (∵ CD is largest side)
∴ ∠ACD < ∠ADC …….(ii)
(Angle opposite to larger side is greater)

Adding equation (i) and (ii)
∠BCA + ∠ACD < ∠BAC + ∠ADC
∠BCD < ∠BAD
or, ∠C < ∠A Similarly by joining B and D we can prove that ∠B > ∠D

Question 5.
In Fig. 7.51, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

Solution:
In ∆PQR
PR > PQ
∠Q > ∠R
Adding ∠1 both side,
∠Q + ∠1 > ∠R + ∠1
or, ∠Q + ∠1 > ∠R + ∠2 (∵ ∠1 = ∠2)
∠PSR > ∠PSQ
(∵ Exterior angle is equal to the sum of opposite interior angles)

Question 6.
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is shortest.
Solution:
Given: A straight line l and a point P not lying on l. PM ⊥ l and N is any point on l other than M.

To prove that: PM < PN
Proof: In ∆PMN, we have
∠M = 90
∠N < 90
(∵ ∠M = 90
⇒ ∠MPN + ∠PNM = 90
⇒ ∠P + ∠N = 90
⇒ ∠N < 90)
⇒∠N< ∠M
⇒ PM < PN (Side opposite to greater angle is larger)
Hence, PM is shortest of all line segments from P to AB.