These NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4 Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
Exercise 2.4
![]()
Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; \(\frac { 1 }{ 2 }\), 1, – 2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:
(i) Comparing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 2, b – 1, c = -5 and d = 2.
Now, we get the zeroes
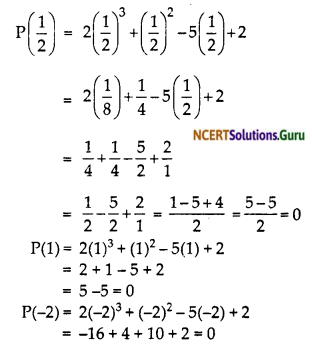
Therefore, \(\frac { 1 }{ 2 }\), 1, – 2 are the zeroes of 2x³ + x² – 5x + 2.
So we take α, ß, γ are the co-efficient of cubic polynomial.
Sum of zeroes

(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Compearing the given polynomial with ax3 + bx2 + cx + d, we get:
a = 1, b = -4, c = 5 and d = – 2.
∴ p (x) = x3 – 4x2 + 5x – 2
⇒ p(2) = (2)3 – 4(2)2 + 5 x 2 – 2
= 8 – 16+ 10 – 2 = 0
p(1) = (1)3 – 4(1)2 + 5 x 1- 2
= 1 – 4 + 1 – 2
= 6 – 6 = 0
Therefore, 2, 1 and 1 are the zeroes of x3 – 4x2 + 5x – 2.
So, take α, ß, γ are the coefficient of cubic polynomial.
Comparing x² – 4x² + 5x – 2 = 0
Sum of zeroes

![]()
Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
We know that a cubic equation is ax³ + bx² + cx + d = 0
But given, α + β + γ = 2
αβ + βγ + γα = -7 and αβγ = – 14
Also, we know that a + b + g = \(\frac { -b }{ a }\) = 2, hence, b = – 2
αβ + βγ + γα = \(\frac { c }{ a }\) = – 7, hence c = – 7 a
αβγ = \(\frac { -d }{ a }\) = – 14, hence d = – 14, and a = 1
Now, put the value of a, b, c, d in equation (1), we get
x³ – 2x² – 7x + 14 = 0
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:
Zeroes of the polynomial are a-b, a, a + b
Sum of zeroes = a-b + a + a + b = 3a

⇒ a³ – b²a = 1
Put a = 1, in a² – b²a = – 1
(1)³ – b² = – 1 ⇒ b² = 2
b= ± \(\sqrt{2}\)
values of a and b are 1, ± \(\sqrt{2}\)
![]()
Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± \(\sqrt{3}\), finnd other zeroes.
Solution:
Let two zeroes are 2 + \(\sqrt{3}\) and 2 – \(\sqrt{3}\),

(x² – 4x +1) is a factor of the given polynomial.
Now, we divide the given polynomial by

So, x4 – 6x3 – 26x2 + 138x – 35 = (x2 – 4x + 1) (x2 – 2x – 35)
Now, by spilitting – 2x, we factorise x² – 2x – 35
= x3 – 7x + 5x – 35
= x(x – 7) (x + 5)
= (x – 7) (x + 5) px = 7, x = – 5
So, zeroes of the given polynomials are
2 + \(\sqrt{3}\), 2 – \(\sqrt{3}\), 7 and – 5.
![]()
Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:
If p(x) and g(x) are any two polynomials of the form x² – 2x and x² + bx + c. We know by formula.
Dividend = Divisor x Quotient + Remainder
x4 – 6x² + 16x3 – 25x + 10 = (x² – 2x + k) (x² + bx + c) + (x + a)
x4 – 6x3 + 16x² – 25x + 10 = x4 + bx3 + x²c – 2x3 – 2bx² – 2cx + kx² + kbx + kc + x + a
x4 – 6x3 + 16x² – 25x + 10 = x4 + (b – 2)x3 + (c – 2b + k) x² + (- 2x + kb + 1)x + kc + a
Now comparing the co-efficients of both sides b – 2 = – 6 … (1)
[Comparing the co-efficient of x3]
c – 2b + k = 16 … (2)
[Comparing the co-efficient of x²]
– 2c + kb + 1 = – 25 … (3)
[Comparing the co-efficient of x]
kc + a = 10 … (4)
[Comparing the constant term]
From (1), b = – 4
Now, putting the vlaue of b in equation (2) and (3) we get,
⇒ c – 2(- 4) + k = 16
or c + k = 8 … (5)
and -2c – 4k + 1 = – 25
or – 2c – 4k = – 26
or – c – 2k = – 13 … (6)
Adding equation (5) and (6), we get, c + k = 8
– c – 2k = – 13 – k = – 5
So, k = 5,
From (5), c = 8 – 5 ⇒ c = 3,
Now put the value of k and c in equation (4), we get,
kc + a = 10
5(3) + a = 10
a = – 5
∴ Value of k and a is 5 and – 5 respectively.
![]()