Author name: Prasanna

These NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities InText Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities InText Questions

Try These (Page No. 119)

Question 1.
In a primary school, the parents were asked about the number of hours they spend per day in helping their children to do homework.
There were 90 parents who helped for \(\frac{1}{2}\) hour to 1\(\frac{1}{2}\) hours. The distribution of parents according to the time for which, they said they helped is given in the following figure: 20% helped for more than 1\(\frac{1}{2}\) hours per day; 30% helped for \(\frac{1}{2}\) hour to 1\(\frac{1}{2}\) hours; 50% did not help at all.
Using this, answer the following:
(i) How many parents were surveyed?
(ii) How many said that they did not help?
(iii) How many said that they helped for man than 1\(\frac{1}{2}\) hours?

Solution:
(i) Since, 30% of total surveyed parents helped their children for “\(\frac{1}{2}\) hours to 1\(\frac{1}{2}\) hours”. And 90 parents helped their children for “\(\frac{1}{2}\) hours to 1\(\frac{1}{2}\) hours”.
30% [ surveyed parents] = 90
or \(\frac{30}{100}\) × [surveyed parents] = 90
or surveyed parents = 90 × 100/30
= 3 × 100
= 300

(ii) Since, 50% of surveyed parents did not help their children.
Number of parents who did not help = 50% of surveyed parents
= 50% of 300
= 50/100 × 300
= 150

(iii) Since, 20% of surveyed parents help their children for more than 1\(\frac{1}{2}\) hours, i.e. 20% of surveyed parents help for more than 1\(\frac{1}{2}\) hours.
Number of parents who helped for more than 1\(\frac{1}{2}\) hours = 20% of 300
= 20/100 × 300
= 20 × 3
= 60
Note: ‘of’ means multiplication

Try These (Page No. 121)

Question 2.
A shop gives a 20% discount. What would the sale price of each of these be?
(a) A dress marked at ₹ 120
(b) A pair of shoes marked at ₹ 750
(c) A bag marked at ₹ 250
Solution:
(a) Marked price of the dress = ₹ 120
Discount rate = 20%
Discount = 20% of ₹ 120
= ₹ \(\frac{20}{100}\) × 120
= ₹ 2 × 12
= ₹ 24
Sale price of the dress = [Marked Price] – [Discount]
= ₹ 120 – ₹ 24
= ₹ 96

(b) Marked price of the pair of shoes = ₹ 750
Discount rate = 20%
Discount = 20% of ₹ 750
= ₹ \(\frac{20}{100}\) × 750
= ₹ 2 × 75
= ₹ 150
Now, Sale price of the pair of shoes = [Marked Price] – [Discount]
= ₹ 750 – ₹ 150
= ₹ 600

(c) Marked price of the bag = ₹ 250
Discount rate = 20%
Discount = 20% of ₹ 250
= ₹ \(\frac{20}{100}\) × 250
= ₹ 2 × 25
= ₹ 50
Sale price of the bag = [Marked price] – [ Discount]
= ₹ 250 – ₹ 50
= ₹ 200

Question 3.
A table marked at ₹ 15,000 is available for ₹ 14,000. Find the discount given and the discount percent.
Solution:
The marked price of the table = ₹ 15000
Sale price of the table = ₹ 14400
Discount = [Marked Price] – [Sale price]
= ₹ 15000 – ₹ 14400
= ₹ 600
Discount percent = Discount/Marked Price × 100

Question 4.
An almirah is sold at ₹ 5,225 after allowing a discount of 5%. Find its marked price.
Solution:
Sale price of the almirah = ₹ 5255
Discount rate = 5%
Since, Discount = 5% of marked price
Marked Price – Discount = Sale price
or [Marked Price] – \(\frac{5}{100}\) × [Marked Price] = Sale price
or [Marked Price] × \(\frac{95}{100}\) = ₹ 5255
or [Marked Price] = ₹ 5255 × \(\frac{95}{100}\) = ₹ 5500

Try These (Page No. 123)

Question 5.
Find selling price (SP) if a profit of 5% is made on
(a) a cycle of ₹ 700 with ₹ 50 as overhead charges.
(b) a lawnmower bought at ₹ 1150 with ₹ 50 as transportation charges.
(c) a fan bought for ₹ 560 and expenses of ₹ 40 made on its repairs.
Solution:
(a) Total cost price = ₹ 700 + ₹ 50 (overhead expenses) = ₹ 750
profit = 5% of ₹ 750
= ₹ \(\frac{5}{100}\) × ₹ 780
= ₹ 5 × \(\frac{15}{100}\)
= ₹ \(\frac{75}{100}\)
= ₹ 37.50
Now, SP = CP + profit
= ₹ 750 + ₹ 37.50
= ₹ 787.50

(b) Total cost price = ₹ 1150 + ₹ 50 (Overhead expenses) = ₹ 1200
Profit = 5% of 1200
= \(\frac{5}{100}\) × ₹ 1200
= ₹ 5 × 12
= ₹ 60
Now, SP = CP + Profit
= ₹ 1200 + ₹ 60
= ₹ 1260

(c) Total cost price = ₹ 560 + ₹ 40 (Overhead expenses) = ₹ 600
Profit = 5% of ₹ 600 = \(\frac{5}{100}\) × ₹ 600
= ₹ 5 × 6
= ₹ 30
Now, SP = CP + profit
= ₹ 600 + ₹ 30
= ₹ 630

Try These (Page No. 123)

Question 6.
A shopkeeper bought two TV sets at ₹ 10,000 each. He sold one at a profit of 10% and the other at a loss of 10%. Find whether he made an overall profit or loss.
Solution:
(a) Marked price of the dress = ₹ 120
Discount rate = 20%
Discount = 20% of ₹ 120
= ₹ \(\frac{20}{100}\) × 120
= ₹ 2 × 12
= ₹ 24
Sale price of the dress = [Marked Price] – [Discount]
= ₹ 120 – ₹ 24
= ₹ 96

(b) Marked price of the pair of shoes = ₹ 750
Discount rate = 20%
Discount = 20% of ₹ 750
= ₹ \(\frac{20}{100}\) × 750
= ₹ 2 × 75
= ₹ 150
Now, Sale price of the pair of shoes = [Marked Price] – [Discount]
= ₹ 750 – ₹ 150
= ₹ 600

(c) Marked price of the bag = ₹ 250
Discount rate = 20%
Discount = 20% of ₹ 250
= ₹ \(\frac{20}{100}\) × 250
= ₹ 2 × 25
= ₹ 50
Sale price of the bag = [Marked price] – [Discount]
= ₹ 250 – ₹ 50
= ₹ 200

Try These (Page No. 126)

Question 7.
Find the interest and amount to be paid on ₹ 15000 at 5% per annum after 2 years.
Solution:
Here P = ₹ 15000, R% = 5%, T = 2 years
Simple Interest = \(\frac{\text { PRT }}{100}\)
= \(\frac{15000 \times 5 \times 2}{100}\)
= ₹ 1500
Amount = ₹ 15000 + ₹ 1500 = ₹ 16,500

Try These (Page No. 129)

Question 8.
Find Cl on a sum of ₹ 8000 for 2 years at 5% per annum compounded annually.
Solution:
We have
P = ₹ 8000, R = 55 p.a., T = 2 years
∴ \(A=P\left[1+\frac{R}{100}\right]^{n}\)
= ₹ 8000 \(\left[1+\frac{5}{100}\right]^{2}\)
= ₹ \(8000\left[\frac{21}{20}\right]^{2}\)
= ₹ \(8000 \times \frac{21}{20} \times \frac{21}{20}\)
= ₹ (20 × 21 × 21)
= ₹ 8820
Now, compound interest = A – P
= ₹ 8820 – ₹ 8000
= ₹ 820

Try These (Page No. 130)

Question 9.
Find the time period and rate for each.
1. A sum taken for 1\(\frac{1}{2}\) years at 8% per annum is compounded half-yearly.
2. A sum taken for 2 years at 4% per annum compounded half-yearly.
Solution:
1. We have interest rate 8% per annum 1\(\frac{1}{2}\) year.
It is compounded half-yearly.
Time period (n) = 2(1\(\frac{1}{2}\)) = 3 half yearly
Rate (R) = \(\frac{1}{2}\) (8%) = 4% per half yearly.

2. We have an interest rate of 4% per annum for the year
Time period (n) = 2(2) = 4 half-yearly
Rate (R) = \(\frac{1}{2}\) (4%) = 2% per half yearly.

Try These (Page No. 131)

Question 10.
Find the amount to be paid
1. At the end of 2 years on ₹ 2,400 at 5% per annum compounded annually.
2. At the end of 1 year on ₹ 1,800 at 8% per annum compounded quarterly.
Solution:
1. We have:
P = ₹ 2400, R = 5% p.a., T = 2 years
∴ Interest is compounded annually i.e, n = 2

2. Here, interest compounded quarterly.
R = 8%, p.a. = \(\frac{8}{4}\), i.e., 2% per quarter
T = 1 year = 4 × 1, i.e., 4 quarters on
n = 4

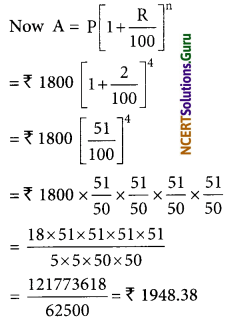
Try These (Page No. 133)

Question 11.
A machinery worth ₹ 10,500 depreciated by 5%. Find its value after one year?
Solution:
Here, P = 10, 500, R = 5% p.a.
T = 1 year, n = 1
∴ A = \(\mathrm{P}\left[1+\frac{5}{100}\right]^{1}\)
[∴ Depreciation is there, r = -5%]
= ₹ \(10500\left[1+\frac{5}{100}\right]^{1}\)
= ₹ 10500 × \(\frac{19}{20}\)
= ₹ 525 × 19
= ₹ 9975
Thus, machinery value after 1 year = ₹ 9975
Note: For depreciation, we use the formula as A = \(\mathrm{P}\left[1-\frac{\mathrm{R}}{100}\right]^{\mathrm{n}}\)

Question 12.
Find the population of a city after 2 years, which is at present 12 lakh, if the rate of increase is 4%.
Solution:
Present population, P = 12 lakh
Rate of increase, R = 4% p.a.
Time, T = 2 years
n = 2
Population after 2 years = \(\mathrm{P}\left[1+\frac{\mathrm{R}}{100}\right]^{\mathrm{n}}\)
= 12 lakh \(\left[1+\frac{4}{100}\right]^{2}\)
= 12 lakh \(\left[\frac{26}{25}\right]^{2}\)
= 12,00, 000 × \(\frac{26}{25} \times \frac{26}{25}\)
= 1920 × 26 × 26
= 12,97,920
Thus, the population of the town will be 12,97,920 after 2 years.

These NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Ex 7.1 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 7 Congruence of Triangles Exercise 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if ……………….
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is ……………….
(c) When we write ∠A = ∠B, we actually mean …………………
Answer:
(a) Two line segments are congruent if they have the same length.
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is 70°.
(c) When we write ∠A ≅ ∠B we actually mean m ∠A = m ∠B.

Question 2.
Give any two real-life examples for congruent shapes.
Answer:
(i) Two ten-rupee notes.
(ii) Biscuits of the same type in the same packet.

Question 3.
If ΔABC ≅ ΔFED under the correspondences ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Answer:
Corresponding vertices : A and F; B and E; C and D.

Corresponding sides : \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{FE}} ; \overline{\mathrm{BC}}\) and \overrightarrow{\mathrm{ED}} ; \overline{\mathrm{CA}} and \(\overline{\mathrm{AB}}\)

Corresponding angles : ∠A and ∠F; ∠B and ∠E; ∠C and ∠D

Question 4.
If ΔDEF ≅ ΔBCA, write the part (s) of ΔBCA that correspond to
(i) ∠E
(ii) \(\overline{\mathrm{EF}}\)
(iii) ∠F
(iv) \(\overline{\mathrm{DF}}\)
Answer:
(i) ∠C
(ii) \(\overline{\mathrm{CA}}\)
(iii) ∠A
(iv) \(\overline{\mathrm{BA}}\)

These NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers InText Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers InText Questions

NCERT In-text Question Page No. 174

Question 1.
Is the number \(\frac{2}{-3}\) rational? Think about it.
Answer:
Yes, \(\frac{2}{-3}\) is a rational number,
∵ 2 and -3 are integers and -3 ≠ 0.

Question 2.
List ten rational numbers.
Answer:
Following are ten rational numbers:
\(\frac{1}{3}, \frac{-2}{3}, \frac{4}{5}, \frac{1}{-6}, \frac{-3}{-4}, 5.8,2 \frac{4}{5}\), 0.93, 18 and 11.07
Note: 1. ‘0’ can be written as \(\frac{0}{2}\) or \(\frac{0}{15}\) etc.
Hence, it is a rational number.
2. A natural number can be written as
5 = \(\frac{5}{1}\) or 108 = \(\frac{108}{1}\) Hence, it is also a rational number.

NCERT In-text Question Page No. 175

Question 1.
Fill in the boxes:

Answer:

Question 2.
Is 5 a positive rational number?
Answer:
Yes, 5 or \(\frac{5}{1}\) is having both its numerator
and denominator as positive.
∴ It is a positive rational number.

Question 3.
List five more positive rational numbers.
Answer:
\(\frac{1}{7}, \frac{3}{8}, \frac{5}{17}, \frac{2}{9}\) and \(\frac{5}{18}\) and are positive rational numbers.

NCERT In-text Question Page No. 176

Question 1.
Is -8 a negative rational number?
Answer:
(i) Yes, -8 or \(\frac{-8}{1}\) is a negative rational number, because its numerator is a negative integer.

Question 2.
List five more negative rational numbers.
Answer:
Five negative rational numbers are as follows:
\(\frac{-5}{9}, \frac{-6}{11}, \frac{-3}{13}, \frac{3}{-10} \text { and } \frac{-1}{7}\)

Question 3.
Which of these are negative rational numbers?
(i) \(\frac{-2}{3}\)
(ii) \(\frac{5}{7}\)
(iii) \(\frac{3}{-5}\)
(iv) 0
(v) \(\frac{6}{11}\)
(vi) \(\frac{-2}{-9}\)
Answer:
(i) \(\frac{-2}{3}\) is a negative rational number.
(ii) \(\frac{5}{7}\) is a positive rational number.
(iii) \(\frac{3}{-5}\) is a negative rational number.
(iv) 0 is neither a positive nor a negative rational number.
(v) \(\frac{6}{11}\) is a positive rational number.
(vi) \(\frac{-2}{-9}\) is a positive rational number.
∴ (i) \(\frac{-2}{3}\) and (ii) \(\frac{3}{-5}\) are negative rational numbers.

NCERT In-text Question Page No. 178

Question 1.
Find the standard form of:
(i) \(\frac{-18}{45}\)
(ii) \(\frac{-12}{18}\)
Answer:
(i) Since HCF of 18 and 45 is 9.
∴ \(\frac{-18}{45}=\frac{(-18) \div 9}{45 \div 9}=\frac{-2}{5}\)
Thus, the standard form of \(\frac{-18}{45}\) is \(\frac{-2}{3}\)

(ii) Since HCF of 12 and 18 is 6.
∴ \(\frac{-12}{18}=\frac{(-12) \div 6}{18 \div 6}=\frac{-2}{3}\)
Thus, the standard form of \(\frac{-12}{18}\) is \(\frac{-2}{3}\)

NCERT In-text Question Page No. 181

Question 1.
Find five rational numbers between \(\frac{-5}{7}\) and \(\frac{-3}{8}\)
Answer:
First we convert the given rational numbers with common denominators,
∴ LCM of 7 and 8 is 56.

Thus, the five rational numbers, between \(\frac{-5}{7}\) and \(\frac{-3}{8}\) are:

NCERT In-text Question Page No. 185

Question 1.
Find:
(i) \(\frac{-13}{7}+\frac{6}{7}\)
(ii) \(\frac{-19}{5}+\frac{-7}{5}\)
Answer:

Question 2.
Find:
(i) \(\frac{-3}{7}+\frac{2}{3}\)
(ii) \(\frac{-5}{6}+\frac{-3}{11}\)
Answer:
(i) \(\frac{-3}{7}+\frac{2}{3}\)
∴ LCM of 7 and 3 is 21

NCERT In-text Question Page No. 186

Question 1.
What will be the additive inverse of \(\frac{3}{9} ?, \frac{-9}{11} ?, \frac{5}{7} ?\)
Answer:
Additive inverse of \(\frac{-3}{9}\) is \(\frac{3}{9}\).
Additive inverse of \(\frac{-9}{11}\) is \(\frac{9}{11}\).
Additive inverse of \(\frac{5}{7}\) is \(\frac{-5}{7}\).

NCERT In-text Question Page No. 187

Question 1.
Find
(i) \(\frac{7}{9}-\frac{2}{5}\)
(ii) \(2 \frac{1}{5}-\left(\frac{-1}{3}\right)\)
Answer:
(i) \(\frac{7}{9}-\frac{2}{5}\)
L.C.M of 9 and 5 is 45.

(ii) \(2 \frac{1}{5}-\left(\frac{-1}{3}\right)\)
L.C.M of 5 and 3 is 15.

NCERT In-text Question Page No. 188

Question 1.
What will be
(i) \(-\frac{3}{5} \times 7\)
(ii) \(-\frac{6}{5} \times(-2) ?\)
Answer:
(i) \(-\frac{3}{5} \times 7=\frac{(-3) \times 7}{5}=\frac{-21}{5}=-4 \frac{1}{5}\)
(ii) \(\frac{-6}{5} \times(-2)=\frac{(-6) \times(-2)}{5}=\frac{12}{5}=2 \frac{2}{5}\)

Question 2.
(i) \(\frac{-3}{4} \times \frac{1}{7}\)
(ii) \(\frac{2}{3} \times \frac{-5}{9}\)
Answer:
(i) \(\frac{-3}{4} \times \frac{1}{7}=\frac{-3 \times 1}{4 \times 7}=\frac{-3}{28}\)
(ii) \(\frac{2}{3} \times \frac{-5}{9}=\frac{-2 \times 5}{3 \times 9}=\frac{-10}{27}\)

NCERT In-text Question Page No. 189

Question 1.
What wTill be the reciprocal of \(\) and \(\) ?
Answer:
Reciprocal of \(\frac{-6}{11}\) is \(\frac{-11}{6}\)
Reciprocal of \(\frac{-8}{5}\) is \(\frac{-5}{8}\)

NCERT In-text Question Page No. 190

Question 1.
Find
(i) \(\frac{2}{3} \times \frac{-7}{8}\)
(ii) \(\frac{-6}{7} \times \frac{5}{7}\)
Answer:
(i) \(\frac{2}{3} \times \frac{-7}{8}=\frac{-7}{12}\)
(ii) \(\frac{-6}{7} \times \frac{5}{7}=\frac{-30}{49}\)

These NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties InText Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 6 The Triangles and Its Properties InText Questions

NCERT In-text Question Page No. 113 & 114
Question 1.
Write the six elements (i.e. the 3 sides and the 3 angles) of ΔABC.
Answer:
Six elements of ΔABC are: ∠A, ∠B, ∠C, \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), and \(\overline{\mathrm{CA}}\).

Question 2.
Write the:
(i) Side opposite to the vertex Q of ΔPQR
(ii) Angle opposite to the side LM of ΔLMN
(iii) Vertex opposite to the side RT of ΔRST
Answer:
(i) The side opposite to the vertex Q is \(\overline{\mathrm{PR}}\).

(ii) The angle opposite to the side LM is ∠N.

(iii) Vertex opposite to the side RT is ‘S’.

Question 3.
Look at figures and classify each of the triangles according to its.
(a) Sides
(b) Angles

Answer:
(i) (a) Since \(\overline{\mathrm{AC}}=\overline{\mathrm{BC}}\) = 8 cm
∴ ΔABC is an isosceles triangle,

(b) Since all angles of ∴ABC are less than 90°.
∴ It is an acute triangle.

(ii) (a) Since PQ ≠ QR ≠ RP
∴ ΔPQR is a scalene triangle.

(b) Since ∠R = 90°
∴ ΔPRQ is a right triangle.

(iii) (a) In ΔLMN, LN = MN = 7 cm
∴ ΔLMN is an isosceles triangle,

(b) In ΔLMN, ∠N > 90°
∴ ΔLMN is an obtuse triangle.

(iv) (a) In ΔRST, RS = ST = TR = 5.2 cm
∴ It is an equilateral triangle.

(b) All the angles of ΔRST are acute.
∴ It is an acute triangle.

(v) (a) In ΔABC, \(\overline{\mathrm{AB}}=\overline{\mathrm{BC}}\) = 3 cm
∴ It is an isosceles triangle.

(b) In ΔABC, ∠B > 90°
∴ It is an obtuse triangle.

(vi) (a) In ΔPQR, latex]\overline{\mathrm{PQ}}=\overline{\mathrm{QR}}[/latex] = 6 cm
∴ It is an isosceles triangle.

(b) In ΔPQR, ∠Q = 90°
∴ It is a right triangle.

NCERT In-text Question Page No. 118
Question 1.
An exterior angle of a triangle is of measure 70° and one of its interior opposite angles is for measure 25°. Find the measure of the other interior opposite angle.
Answer:
Exterior angle = 70°
Interior opposite angles are 25° and x.
∴ x + 25° = 70°
[Using the exterior angle property of a triangle]
or x = 70°- 25°= 45°
∴ The required interior opposite angle = 45°.

Question 2.
The two interior opposite angles of an exterior angle of triangle are 60° and 80°. Find the measure of the exterior angle.
Answer:
Interior angles are 60° and 80°.
∵ [Exterior angle] = 60° + 80° = 140°

Question 3.
Is something wrong in this diagram?

Answer:
We know that an exterior angle of a triangle is equal to the sum of interior opposite angles. Here interior angles are 50° each and exterior angle is 50°.
∴ This triangle cannot be formed.
[∵ 50° ≠ 50° + 50°]

NCERT In-text Question Page No. 122
Question 1.
Two angles of a triangle are 30° and 80°. Find the third angle.
Answer:
Let the third angle be x.
∴ Using the angle sum property of a triangle,
30° + 80° + x = 180°
or x + 110° = 180°
or x = 180°- 110° = 70°
∴ The measure of the required third angle is 70°.

Question 2.
One of the angles of a triangle is 80° and the other two angles are equal. Find the measure of each of the equal angles.
Answer:
Let each of the equal angles be x
x + x + 80° = 180°
(angle sum property of a triangle)
2x + 80° = 180°
2x = 180° – 80°
2x = 100°
x = \(\frac{100^{\circ}}{2}\) = 50°
∴ The required measure of each of the equal angle is 50°.

Question 3.
The three angles of a triangle are in the ratio 1:2:1. Find all the angles of the triangle. Classify the triangle in two different ways.
Answer:
Let the three angles of a triangle be x, 2x and x
x + 2x + x = 180°
(using the angle sum property)
2x + 2x = 180°
4x = 180°
x \(\frac{180^{\circ}}{4}\) = 45°
Thus, the three angles are 45°, 90° and 45°. It is an isosceles triangle (two angles are equal, opposite sides also equal)
As one angle is 90°.
∴ It is a right-angled triangle.

NCERT In-text Question Page No. 123 & 124
Question 1.
Find angle x in each figure:





Answer:
(i) Since the two sides in the triangle are equal, the base angle opposite to equal sides are equal.
∴ x = 40°

(ii) Since the two sides of the triangle are equal, the base angles opposite to equal sides are equal so, the other angle = 45°
Sum of three angles of a triangle = 180°
45° + 45° + x = 180°
x + 90° = 180°
x = 180° – 90°
x = 90°

(iii) Since the two sides of the triangle are equal, the base angles opposite to equal sides are equal.
x = 50°

(iv) Base angles opposite to the equal sides of an isosceles triangle are equal and the sum of the measures of the three angles is 180°.
100° + x + x = 180°
2x = 180° – 100°
2x = 80°
x = \(\frac{80^{\circ}}{2}\) = 40°

(v) Base angles opposite to the equal sides of an isosceles triangles are equal and the sum of the measure of three angles of triangle is 180°.
x + x + 90° = 180°
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac{90^{\circ}}{2}\) = 45°

(vi) Base angles opposite to the equal sides of an isosceles triangle are equal and the sum of the measures of the three angles of triangle is 180°.
x + x + 40° = 180°
2x + 40° = 180°
2x = 180° – 40°
2x = 140°
x = \(\frac{140^{\circ}}{2}\)
= 70°
x = 70°

(vii) In the figure, two sides of the triangle are equal.
∴ The base angles opposite to equal sides are equal one of the base angle = x
other base angle = x
Now, x° and 120° form a linear pair = 180°
x + 120° = 180°
x = 180° -120°
= 60°
Thus, the value of x = 60°

(viii) In the figure, two sides of the triangle are equal.
since, one of the base angles = x
∴ The other base angle = x
Since, exterior angle is equal to sum of the interior opposite angles
∴ x + x = 110°
2x = 110°
x = \(\frac{110^{\circ}}{2}\) = 55°

(ix) Two sides of the triangle are equal.
∴ The base angles opposite to the equal sides are equal.
Since, one of the base angle = x
∴ The other base angle = x
Also, the vertically opposite angles 30° and x are equal.
∴ x = 30°

Question 2.
Find angles x and y in each figure.

Answer:
(i) Two sides of the triangle are equal.
∴ The base angles opposite to the equal sides are equal.
The other base angle is y.
Now y and 120° form a linear pair.
∴ y + 120° = 180°
y = 180° – 120° = 60°
∴ x + y + y = 180°
(sum of the three angles = 180°)
x + 60° + 60°= 180°
x+ 120° = 180°
x = 180° – 120°
= 60°
Thus x = 60° and y = 60°

(ii) Two sides of a triangles are equal.
∴ The base angles opposite to equal sides are equal. Since one of the base angle is ‘x’
∴ The other base angle = x
The given triangle is a right-angled triangle.
x + x + 90° = 180°
2x + 90° = 180°
2x = 180° – 90°
2x = 90°
x = \(\frac{90^{\circ}}{2}\) = 45°
Now x and y form a linear pair
x + y = 180°
45°+ y = 180°
y = 180° – 45° = 135°
Thus, x = 45° and y = 135°

(iii) In the given figure, two sides of a triangle are equal.
∴ The base angles are x and x
The third angle = 92°
(vertically opposite angles are equal)
x + x + 92° = 180°
(Sum of the three angles of a triangle is 180°)
2x + 92° = 180°
2x = 180° – 92°
2x = 88°
x = \(\frac{88^{\circ}}{2}\) = 44°
Now, x and y form a linear pair
x + y = 180°
44 + y = 180°
y = 180° – 44° = 136°
Thus, x = 44° and y = 136°

NCERT In-text Question Page No. 129 & 130
Question 1.
Find the unknown length x in the following figures.



(i) In the given right-angled triangle, the longest side (hypotenuse) is x
x² = 3² + 4²
(using pythagoras property)
= 9 + 16
= 25
or x² = 5²
x = \(\sqrt{25}\)
= 5
x = 5

(ii) The given figure is a right-angled triangle.
x² = 6² + 8²
(using pythagoras property)
= 36 + 64
x² = 100
x² = 10²
∴ x = 10

(iii) The given figure is a right-angled triangle.
x² = 8² + 15²
(using pythagoras property)
x² = 64 + 225
x² = 289
x² = 17²
x = 17

(iv) The given figure is a right-angled triangle
x² = 7² + 24²
(using pythagoras property)
x² = 49 + 576
x² = 625
x² = 25²
x = 25

(v) The given figure can be labelled as ΔABC and the altitude is AD. Consider the right-angled triangle ABD
AB² = AD² + BD²
(using pythagoras property)

37² = 12² + BD²
1369 = 144 + BD²
1369 – 144 = BD²
1225 = BD²
35² = BD²
∵ BD = 35
In the right-angled triangle ADC
AC² = AD² + DC²
(using pythagoras property)
37² = 12² + DC²
1369 = 144 +DC²
1369 – 144 = DC²
1225 = DC²
35² = DC²
∴ DC = 35
∵ BC = BD + DC
= 35 + 35
x = 70

(vi) In the given right-angled triangle
x² = 12² + 5²
(using the pythagoras property)
= 144 + 25
x² = 169
x² = 13²
∴ x = 13

These NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.2 Questions and Answers are prepared by our highly skilled subject experts.

NCERT Solutions for Class 7 Maths Chapter 9 Rational Numbers Exercise 9.2

Question 1.
Find the sum:

Answer:

Question 2.

Answer:

|

Question 3.
(i) \(\frac{9}{2} \times\left(\frac{-7}{4}\right)\)
(ii) \(\frac{3}{10} \times(-9)\)
(iii) \(\frac{-6}{5} \times \frac{9}{11}\)
(iv) \(\frac{3}{7} \times\left(\frac{-2}{5}\right)\)
(v) \(\frac{3}{11} \times \frac{2}{5}\)
(vi) \(\frac{3}{-5} \times \frac{-5}{3}\)
Answer: