CBSE Class 12

These NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.2 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-8-ex-8-2/

NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals Exercise 8.2

Ex 8.2 Class 12 NCERT Solutions Question 1.
Find the area of the circle 4x² + 4y² = 9 which is interior to the parabola x² = 4y.
Solution:

4x² + 4y² = 9
∴ x² + y² = \(\frac { 9 }{ 4 }\) … (1) is a circle with
centre (0,0) and radius = \(\frac { 3 }{ 2 }\)
x² = 4y … (2)
Substituting (2) in (1), we get 4y + y²
⇒ 4y² + 16y – 9 = 0
⇒ 4y² – 2y + 18y – 9 = 0
⇒ 2y(2y – 1) + 9(2y – 1) = 0
⇒ (2y – 1)(2y + 9) = 0
⇒ y = \(\frac { 1 }{ 2 }\), y = \(\frac { – 9 }{ 2 }\)
∴ y = \(\frac { 1 }{ 2 }\)
Substitute y = \(\frac { 1 }{ 2 }\) in (2) we get x = ± \(\sqrt{2}\)
∴ The point of intersection of the curves are (- \(\sqrt{2}\), \(\frac { 1 }{ 2 }\)) and (\(\sqrt{2}\), \(\frac { 1 }{ 2 }\))
Since the shaded region is symmetric with respect to y-axis,
Required Area = 2[Area under the circle – Area under the parabola] lying in the first quadrant between the lines x = 0 and x = \(\sqrt{2}\)

Exercise 8.2 Class 12 NCERT Solutions Question 2.
Find the area bounded by curves (x – 1)² + y² = 1 and x² + y² = 1.
Solution:

x² + y² = 1 is a circle with centre at origin and intersecting positive x-axis at (1, 0).
(x – 1)² + y = 1 is a circle with centre at the origin and passing through the origin.
Solving x² + y² = 1 and (x – 1)² + y² = 1,
we get x² – (x – 1)² = 0
(x – x + 1)(x + x – 1) = 0
2x – 1 = 0
∴ x = \(\frac { 1 }{ 2 }\)
When x = \(\frac { 1 }{ 2 }\), we get (\(\frac { 1 }{ 2 }\))² + y² = 1
y² = \(\frac { 3 }{ 4 }\)
∴ y = \(\frac{\pm \sqrt{3}}{2}\)
Hence the points of intersection of the two circles are (\(\frac { 1 }{ 2 }\), \(\frac{\pm \sqrt{3}}{2}\)) and (\(\frac { 1 }{ 2 }\), \(\frac{\pm \sqrt{- 3}}{2}\)).
The area bounded by the two curves is sym-metric w.r.t. x-axis.
∴ Required area = 2 x shaded area … (1)
Area of shaded region = Area under arc OA + Area under arc AC

8.2 Class 12 NCERT Solutions Question 3.
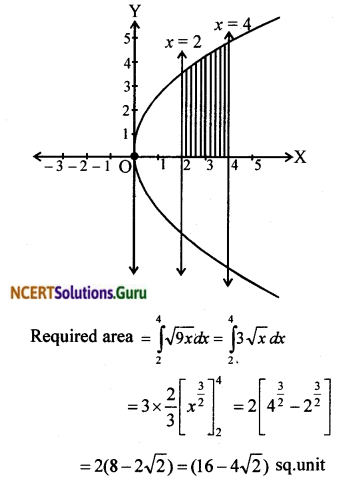
Find the area of the region bounded by the curves y = x² + 2, y = x, x = 0 and x = 3.
Solution:
Equation of the parabola is y = x² + 2 or x² = (y – 2)
Its vertex is (0,2) axis is y-axis.
Boundary lines are y = x, x = 0, x = 3.
Graphs of the curve and lines have been shown in the figure.
Area of the region PQRO = Area of the region OAQR – Area of region OAP

Ex 8.2 Class 12 Maths Ncert Solutions Question 4.
Using integration find the area of region bounded by the triangle whose vertices are (-1, 0), (1, 3) and (3, 2).
Solution:
Let the vertices of the triangle are A(- 1, 0), B(1, 3) and C(3, 2).

Equation of AB is y – 0 = \(\frac { 3 – 0 }{ 1+1 }\)(x+1)
i.e, y = \(\frac { 3 }{ 2 }\)(x + 1)
Equation of BC is y – 3 = \(\frac { 2 – 3 }{ 3 – 1 }\)(x – 1)
i.e, y – 3 = \(\frac { – 1 }{ 2 }\)(x – 1) ∴ y = \(\frac { 7 – x }{ 2 }\)
Equation of AC is y – 0 = \(\frac { 2 – 0 }{ 3 + 1 }\) (x + 1)
i.e., y = \(\frac { 1 }{ 2 }\)(x + 1)
Area of ∆ ABC = Area of ∆ ADB + Area of trapezium BDEC – Area of ∆ AEC

Exercise 8.2 Class 12 Maths Ncert Solutions Question 5.
Using integration find the area of the triangular region whose sides have the equations y = 2x + 1,y = 3x + 1 and x = 4.
Solution:
The equations of sides of the triangle are
y = 2x+ 1 … (1), y = 3x + 1 … (2), x = 4 … (3)
Solving equations (1) and (2), we get x = 0 and y = 1
Let A be the point (0,1)
Solving equations (1) and (3), we get x = 4 and y = 9.
Let B be the point (4, 9) Solving equations (2) and (3) we get x = 4 and y = 13
Let C be the point (4, 13)

Ex 8.2 Class12 NCERT Solutions Question 6.
Smaller area bounded by the circle x² + y² = 4 and the line x + y = 2
(a) 2 (π – 2)
(b) π – 2
(c) 2π – 1
(d) 2(π + 2)
Solution:
x² + y² = 4 intersects the positive x-axis at (2, 0) and the positive y-axis at (0, 2). The line x + y = 2 passes through (2, 0) and (0, 2).

Required area is shaded in the figure. Required Area = (Area of circle – Area under the line) lying in the first quadrant

Ex 8.2 Class 12 Ncert Solutions Question 7.
Area lying between the curves y² = 4x and y = 2x.
(a) \(\frac { 2 }{ 3 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 1 }{ 4 }\)
(d) \(\frac { 3 }{ 4 }\)
Solution:
(b) \(\frac { 1 }{ 3 }\)

The given curves are y² = 4x … (1)
y = 2x … (2)
4x(x – 1) = 0 ⇒ x = 0, x = 1
When x = 0, y = 0
When x = 1, y = 2
The points of intersection are (0, 0) and (1, 2)
Required area is shaded in the figure.

These NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals Ex 8.1 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-8-ex-8-1/

NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals Exercise 8.1

Question 1.
Find the area of the region bounded by the curve y² = x and the lines x = 1, x = 4, and the x-axis.
Solution:
The required area is shaded in the figure and lies between the lines x = 1 and x = 4. Hence the limits of integration are 1 and 4.

Question 2.
Find the area of the region bounded by y² = 9x, x = 2, x = 4 and x-axis in the first quadrant
Solution:
The required area is shaded in the figure lies between the lines x = 2 and x = 4. Hence the limits of integration are 2 and 4.

Question 3.
Find the area of the region bounded by x² = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Solution:
x² = 4y ∴ x = 2\(\sqrt{y}\)
The required area is shaded in the figure and lies between the lines y = 2 and y = 4. Hence the limits of integration are 2 and 4.

Question 4.
Find the area of the region bounded by the ellipse \(\frac { { x }^{ 2 } }{ 16 } +\frac { { y }^{ 2 } }{ 9 }\) = 1
Solution:
i. Put y = o in \(\frac { { x }^{ 2 } }{ 16 } +\frac { { y }^{ 2 } }{ 9 }\) = 1, we get \(\frac{x^{2}}{16}=1\)
i.e., x² = 16 ∴ x = ± 4
∴ The points of intersection with x-axis are (-4, 0) and (4, 0)

ii. The shaded area lies between x = 0 and x = 4.
∴ The limits of integration are 0 and 4.
The curve is symmetrical w.r.t both the axes
∴ Required area = 4 x area of the shaded region
\(\frac { { x }^{ 2 } }{ 16 } +\frac { { y }^{ 2 } }{ 9 }\) = 1 i.e., \(\frac{y^{2}}{9}=1\) – \(\frac{x^{2}}{16}=1\)

Question 5.
Find the area of the region bounded by the ellipse \(\frac { { x }^{ 2 } }{ 4 } +\frac { { y }^{ 2 } }{ 9 } \) = 1
Solution:

The points of intersection of the curve and the x-axis is obtained by substituting y = 0 in the equation of the curve.
We get \(\frac{x^{2}}{4}=1\), x² = 4 ∴ x = ±2
The curve intersects the x-axis at (-2, 0) and (2,0).
\(\frac { { x }^{ 2 } }{ 4 } +\frac { { y }^{ 2 } }{ 9 } \) = 1 ∴ \(\frac{y^{2}}{9}\) = 1 – \(\frac{x^{2}}{4}=1\)
= \(\frac{4-x^{2}}{4}\)
∴ y² = \(\frac { 9 }{ 4 }\)(4 – x²) ∴ y = \(\frac{3}{2} \sqrt{4-x^{2}}\)
The curve is symmetrical about both the axes.
Area of the ellipse = 4 x area of the shaded region

Question 6.
Find the area of the region in the first quadrant enclosed by x-axis, line x = \(\sqrt{3}\)y and the circle x² + y² = 4.
Solution:

The given equations are x = \(\sqrt{3}\)y … (1)
x² + y = 4 … (2)
To get the point of intersection of the line and the circle, solve (1) and (2)
From (1), we get y = \(\frac{x}{\sqrt{3}}\)
∴ (2) → x² + \(\left(\frac{x}{\sqrt{3}}\right)^{2}\) = 4 ⇒ x² + \(\frac{x^{2}}{3}\) = 4
\(\frac{4x^{2}}{3}\) = 4 ⇒ x² = 3 ⇒ x = ±\(\sqrt{3}\)
To get the point of intersection of the circle and x-axis puty = 0 in (2)
(2) → x² = 4 ∴x = ± 2
∴ The x coordinate of A and B are \(\sqrt{3}\) and 2 respectively.
Required area = Area of OAC + Area of ACB

Question 7.
Find the area of the smaller part of the circle x² + y² = a² cut off by the line x = \(\frac { a }{ \sqrt { 2 } }\).
Solution:

x² + y² = a² is a circle which intersects the positive x axis at (a, 0).
x² + y² = a²
∴ y = \(\sqrt{a^{2}-x^{2}}\)
The required area is shaded in the figure and lies between x = \(\frac { a }{ \sqrt { 2 } }\) and x – a
∴ Limits of integration are \(\frac { a }{ \sqrt { 2 } }\) and a
Area of the shaded region = 2 x Area of the shaded region in the first quadrant

Question 8.
The area between x = y² and x = 4 is divided into two equal parts by the line x = a, find the value of a.
Solution:

The given curves are x = y² … (1)
x = 4 ….. (2) and x = a … (3)
Since the line x = a divides the area in two equal parts, we get \(2 \int_{0}^{a} y d x=2 \int_{a}^{4} y d x\)
Since the areas are symmetric w.r.t. x-axis

Question 9.
Find the area of the region bounded by the parabola y = x² and y = |x|.
Solution:
Clearly x² = y represents a parabola with vertex at (0, 0) positive direction of y-axis as its axis it opens upwards.
y = |x| i.e., y = x and y = – x represent two lines passing through the origin and making an angle of 45° and 135° with the positive direction of the x-axis.
The required region is the shaded region as shown in the figure. Since both the curve are symmetrical about y-axis.
So,
Required area = 2 (shaded area in the first quadrant)

Question 10.
Find the area bounded by the curve x² = 4y and the line x = 4y – 2
Solution:

The given curves are x² = 4y … (1)
and x – 4y – 2 … (2)
Substituting (2) in (1),
we get (4y – 2)² = 4y
⇒ 16y² – 16y + 4 = 4y
⇒ 16y² – 20y + 4 = 0
⇒ 4y² – 5y + 1 = 0
⇒ 4y² – 4y – y + 1 = 0
⇒ 4y(y – 1) – 1(y – 1) = 0
⇒ (y – 1)(4y – 1) = 0
⇒ y = 1, y = \(\frac { 1 }{ 4 }\)
When y = 1, x = 2
When y = \(\frac { 1 }{ 4 }\), x = – 1
∴ Points of intersection are (-1, \(\frac { 1 }{ 4 }\)) and (2, 1)
The required area is shaded in the figure. Required area = (Area under the line x = 4y – 2) – (Area under the parabola x² = 4y) :

Question 11.
Find the area of the region bounded by the curve y² = 4x and the line x = 3.
Solution:

The given curves are y² = 4x … (1)
and x = 3
The shaded region is symmetric w.r.t. x-axis.
∴ Required area = 2 x Shaded area in the first quadrant

Question 12.
Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is
(a) π
(b) \(\frac { \pi }{ 2 } \)
(c) \(\frac { \pi }{ 3 } \)
(d) \(\frac { \pi }{ 4 } \)
Solution:
(a) π

Question 13.
Area of the region bounded by the curve y² = 4x, y-axis and the line y = 3 is
(a) 2
(b) \(\frac { 9 }{ 4 }\)
(c) \(\frac { 9 }{ 3 }\)
(d) \(\frac { 9 }{ 2 }\)
Solution:

These NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.11 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-7-ex-7-11/

NCERT Solutions for Class 12 Maths Chapter 7 Integrals Exercise 7.11

Ex 7.11 Class 12 NCERT Solutions Question 1.
\(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ { cos }^{ 2 }x\quad dx }\)
Solution:

7.11 Class 12 NCERT Solutions Question 2.
\(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { \sqrt { sinx } }{ \sqrt { sinx } +\sqrt { cosx } } dx } \)
Solution:

Exercise 7.11 Maths Class 12 Question 3.
\(\int_{0}^{\frac{\pi}{2}} \frac{\sin ^{\frac{3}{2}} x d x}{\sin ^{\frac{3}{2}} x+\cos ^{\frac{3}{2}} x}\)
Solution:

7.11 Maths Class 12 NCERT Solutions Question 4.
\(\int_{0}^{\frac{\pi}{2}} \frac{\cos ^{5} x d x}{\sin ^{5} x+\cos ^{5} x}\)
Solution:

Exercise 7.11 Class 12  Question 5.
\(\int_{-5}^{5}|x+2| d x\)
Solution:
|x+2| = x + 2 if x + 2 ≥ 0 ⇒ x ≥ – 2
|x+2| = -(x + 2) if x + 2 < 0 ⇒ x < – 2

Ex 7.11 Class 12 Maths Ncert Solutions Question 6.
\(\int_{2}^{8}|x-5| d x\)
Solution:

Ex7.11 Class 12 NCERT Solutions Question 7.
\(\int _{ 0 }^{ 1 }{ x(1-x)^{ n }dx } =I\)
Solution:

Class 12 Ex 7.11 NCERT Solutions Question 8.
\(\int _{ 0 }^{ \frac { \pi }{ 4 } }{ log(1+tanx)dx } \)
Solution:

7.11 Class 12 Maths Question 9.
\(\int_{0}^{2} x \sqrt{2-x} d x\)
Solution:

Class 12 Maths Exercise 7.11 Solutions Question 10.
\(\int_{0}^{\frac{\pi}{2}}(2 \log \sin x-\log \sin 2 x)\)dx
Solution:

Question 11.
\(\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin ^{2} x d x\)
Solution:
Here f(x) = sin²x
∴ f(x) = sin²(-x) = [sin(-x)]²
= (-sinx)² = sin²x
Since f(-x) = f(x),
f(x) = sin²x is an even function.

Question 12.
\(\int_{0}^{\pi} \frac{x d x}{1+\sin x}\)
Solution:

Question 13.
\(\int _{ \frac { -\pi }{ 2 } }^{ \frac { \pi }{ 2 } }{ { sin }^{ 7 } } xdx\)
Solution:
Let f(x) = sin⁷ xdx
⇒ f(-x) = -sin⁷ x = -f(x)
⇒ f(x) is an odd function of x
⇒ \(\int _{ \frac { -\pi }{ 2 } }^{ \frac { \pi }{ 2 } }{ { sin }^{ 7 } } xdx=0\)

Question 14.
\(\int _{ 0 }^{ 2\pi }{ { cos }^{ 5 } } xdx\)
Solution:
Let f(x) = cos⁵ x
f(2π – x) = cos⁵(2π – x) = cos⁵ x
f(2π – x) = f(x)

Question 15.
\(\int _{ 0 }^{ \frac { \pi }{ 2 } }{ \frac { sinx-cosx }{ 1+sinx\quad cosx } dx } \)
Solution:

Question 16.
\(\int_{0}^{\pi} \log (1+\cos x) d x\)
Solution:

Question 17.
\(\int_{0}^{a} \frac{\sqrt{x}}{\sqrt{x}+\sqrt{a-x}} d x\)
Solution:

Question 18.
\(\int_{0}^{4}|x-1| d x\)
Solution:

Question 19.
Show that \(\int_{0}^{a} f(x) g(x) d x=2 \int_{0}^{a} f(x) d x\) if f and g are defined as f(x) = f(a – x) and g(x) + g(a – x) = 4
Solution:

Question 20.
The value of
\(\int _{ \frac { -\pi }{ 2 } }^{ \frac { \pi }{ 2 } }{ \left( { x }^{ 3 }+xcosx+{ tan }^{ 5 }x+1 \right) dx } \) is
(a) 0
(b) 2
(c) π
(d) 1
Solution:
(c) π
Let f(x) = x³ + x cosx + tan⁵x
f(- x) = (- x)³ + (- x)cos(- x) + tan5(- x)
= – x³ – x cosx – tan5x
= – f(x)
∴ f(x) is an odd function

Question 21.
The value of \(\int_{0}^{\frac{x}{2}} \log \left(\frac{4+3 \sin x}{4+3 \cos x}\right) d x\) is
(a) 2
(b) \(\frac { 3 }{ 4 }\)
(c) 0
(d) – 2
Solution:

I = – 1
2I = 0 Hence I = 0
Evaluate the following.

These NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.8 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-7-ex-7-8/

NCERT Solutions for Class 12 Maths Chapter 7 Integrals Exercise 7.8

Question 1.
\(\int_{a}^{b} x d x\)
Solution:
Let I = \(\int_{a}^{b} x d x\)
f(x) = x, nh = b – a
f(a) = a
f[a + h) = a + h
f(a + 2 h) = a+ 2h,
……………………….
f[a + (n – 1)h) = a + (n – 1)h

Question 2.
\(\int_{0}^{5}(x+1) d x\)
Solution:
Let I = \(\int_{0}^{5}(x+1) d x\)
We have a = 0, b = 5 and f(x) = x + 1
nh = b-a = 5 – 0 = 5
f(0) = 0 + 1 = 1
f(0 + h) = 0 + h + 1 = h + 1
f(0 + 2h) = 0 + 2h + 1 = 2h + 1
………………………….
f(0 + (n – 1 )h) = 0 + (n – 1)h + 1 = (n – 1)h + 1

Question 3.
\(\int_{2}^{3} x^{2} d x\)
Solution:
Let I = \(\int_{2}^{3} x^{2} d x\)
f(x) = x², a = 2, b = 3, nh = b – a = 3 – 2 = 1
f(2) = 2² = 4,
f(2 + h) = (2 + h)² = 4 + h² + 4h
f(2 + 2h) = (2 + 2h)² = 4+ 4h² + 8h
………………………….
f(2 + (n – 1 )h) = (2 + (n – 1)h]² = 4 + (h – 1)²h² + 4(n – 1)h

Question 4.
\(\int_{1}^{4}\left(x^{2}-x\right) d x\)
Solution:
Let I = \(\int_{1}^{4}\left(x^{2}-x\right) d x\)
We have a = 1, b = 4, f(x) = x² – x and nh = b – a = 4 – 1 = 3
f(1) = 1² – 1 = 0
f(1 + h) = (1 + h)² – (1 + h) = h² + h
f(1 + 2h) = (1 + 2h)² – (1 + 2 h) = 2²h² + 2 h
………………………….
f(1 + n – 1)h) = [1 + (n – 1)h]² – [1 + (n – 1)h] = (n – 1)² h² +(n – 1 )h

Question 5.
\(\int_{-1}^{1} e^{x} d x\)
Solution:
Let I = \(\int_{-1}^{1} e^{x} d x\)
We have a = – 1, b = 1, f(x) = e^x, nh = b – a = 1 + 1 = 2
f(- 1) = e^-1
f(- 1 + h) = e^-1+h
f(- 1 + 2h) = e^-1+2h
………………………….
f(- 1 + (n – h)h) = e^-1+(n-1)h

Question 6.
\(\int_{0}^{4}\left(x+e^{2 x}\right) d x\)
Solution:
Let I = \(\int_{0}^{4}\left(x+e^{2 x}\right) d x\)
f(x) = x + e^2x
a = 0, b = 4, nh = b – a = 4 – 0 = 4
f(0) = 0 + e⁰ = 1
f(0 + h) = (0 + h) + e^2(0+h) = h + e^2h
f(0 + 2h) = (0 + 2h) + e^2(0+h) = 2h + e^2h
………………………….
f(0 + (n – 1)h) = (0 + (n – 1 )h) + e^2(0+h)=(n – 1 )h + e^2(n-1)h

These NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.4 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-7-ex-7-4/

NCERT Solutions for Class 12 Maths Chapter 7 Integrals Exercise 7.4

Maths Class 12 Chapter 7 Exercise 7.4 Question 1.
\(\frac { { 3x }^{ 2 } }{ { x }^{ 6 }+1 } \)
Solution:
Let x³ = t ⇒ 3x²dx = dt
\(\int { \frac { { 3x }^{ 2 } }{ { x }^{ 6 }+1 } dx } =\int { \frac { dt }{ { t }^{ 2 }+1 } } ={ tan }^{ -1 }t+C\)
= tan^-1 (x³) + C

Question 2.
\(\frac { 1 }{ \sqrt { 1+{ 4x }^{ 2 } } } \)
Solution:

Question 3.
\(\frac { 1 }{ \sqrt { { (2-x) }^{ 2 }+1 } } \)
Solution:

Question 4.
\(\frac { 1 }{ \sqrt { 9-{ 25x }^{ 2 } } } \)
Solution:

Question 5.
\(\frac { 3x }{ 1+{ 2x }^{ 4 } } \)
Solution:

Question 6.
\(\frac { { x }^{ 2 } }{ 1-{ x }^{ 6 } } \)
Solution:
put x³ = t,so that 3x²dx = dt
\(\int { \frac { { x }^{ 2 } }{ 1-{ x }^{ 6 } } dx } \quad =\frac { 1 }{ 3 } \int { \frac { dt }{ 1-{ t }^{ 2 } } \quad =\frac { 1 }{ 6 } log } \left| \frac { 1+t }{ 1-t } \right| +C\)
\(=\frac { 1 }{ 6 } log\left| \frac { 1+{ x }^{ 3 } }{ 1-{ x }^{ 3 } } \right| \) + C

Question 7.
\(\frac { x-1 }{ \sqrt { { x }^{ 2 }-1 } } \)
Solution:

Question 8.
\(\frac { { x }^{ 2 } }{ \sqrt { { x }^{ 6 }+{ a }^{ 6 } } } \)
Solution:

Question 9.
\(\frac { { sec }^{ 2 }x }{ \sqrt { { tan }^{ 2 }x+4 } } \)
Solution:

Question 10.
\(\frac { 1 }{ \sqrt { { x }^{ 2 }+2x+2 } } \)
Solution:

Question 11.
\(\frac { 1 }{ { 9x }^{ 2 }+6x+5 } \)
Solution:

Question 12.
\(\frac { 1 }{ \sqrt { 7-6x-{ x }^{ 2 } } } \)
Solution:

Question 13.
\(\frac { 1 }{ \sqrt { (x-1)(x-2) } } \)
Solution:

Question 14.
\(\frac { 1 }{ \sqrt { 8+3x-{ x }^{ 2 } } } \)
Solution:

Question 15.
\(\frac { 1 }{ \sqrt { (x-a)(x-b) } } \)
Solution:

Question 16.
\(\frac { 4x+1 }{ \sqrt { { 2x }^{ 2 }+x-3 } } \)
Solution:

Question 17.
\(\frac { x+2 }{ \sqrt { { x }^{ 2 }-1 } } \)
Solution:

Question 18.
\(\frac { 5x-2 }{ 1+2x+{ 3x }^{ 2 } } \)
Solution:
Let 5x – 2 = A(6x + 2) + B … (1)
Equating the coefficients of x, we get
6A = 5 ⇒ A = \(\frac { 5 }{ 6 }\)
Equating the constant terms, we get
2A + B = – 2 ⇒ B = – 2 – 2A
= – 2 – \(\frac { 5 }{ 3 }\) = \(\frac { – 11 }{ 3 }\)
∴ (1) → 5x – 2 = \(\frac { 5 }{ 6 }\) (6x + 2) – \(\frac { 11 }{ 3 }\)

Question 19.
\(\frac { 6x+7 }{ \sqrt { (x-5)(x-4) } } \)
Solution:
∫\(\frac { 6x+7 }{ \sqrt { (x-5)(x-4) } } \)dx = \(\int \frac{6 x+7}{\sqrt{x^{2}-9 x+20}} d x\)
Let 6x + 7 = A\(\frac { d }{ dx }\)(x² – 9x + 20) + B
6x + 7 = A(2x – 9) + B
Equating coefficients of x, we get
2A = 6 ⇒ A = 3
Equating the constant terms,
we get 7 = – 9A + B
= B = 7 + 9A ⇒ B = 7 + 27 = 34
i.e, 6x + 7 = 3(2x – 9) + 34

Question 20.
\(\frac { x+2 }{ \sqrt { 4x-{ x }^{ 2 } } } \)
Solution:
Let x + 2 = A\(\frac { d }{ dx }\)(4x – x²) + B
x + 2 = A(4 – 2x) + B.
Equating coeffleints of x and constants an both sides, we get
– 2A = 1 ⇒ A = \(\frac {- 1 }{ 2 }\) and 4A + B = 2
⇒ B = 2 – 4A
⇒ B = 2 – 4\(\frac {- 1 }{ 2 }\) = 4
i.e., x + 2 = \(\frac {- 1 }{ 2 }\)(4 – 2x) + 4

Question 21.
\(\frac { x+2 }{ \sqrt { { x }^{ 2 }+2x+3 } } \)
Solution:
∫\(\frac { x+2 }{ \sqrt { { x }^{ 2 }+2x+3 } } \)dx
Let x + 2 = A\(\frac { d }{ dx }\)(x² + 2x + 3) + B
x + 2 = A(2x + 2) + B
Equating coefficients of x and constant terms on both sides, we get
2A = 1 ⇒ A = \(\frac { 1 }{ 2 }\) and 2A + B = 2
⇒ B = 2 – 4A
⇒ B = 2 – 2\(\frac { 1 }{ 2 }\) = 2 – 1 = 1
i.e., x + 2 = \(\frac { 1 }{ 2 }\)(2x + 2) + 1

Question 22.
\(\frac { x+3 }{ { x }^{ 2 }-2x-5 } \)
Solution:
Let x + 3 = A(2x – 1) + B
Equating coeffleints of x and constants an both sides, we get 2A = 1 ⇒ A = \(\frac { 1 }{ 2 }\)
Equating the constant terms, we get – 2A + B = 3 ⇒ B = 4 ∴ A = \(\frac { 1 }{ 2 }\), B = 4

Question 23.
\(\frac { 5x+3 }{ \sqrt { { x }^{ 2 }+4x+10 } } \)
Solution:
Let 5x + 3 = A\(\frac { d }{ dx }\)(x² + 4x + 10) + B
5x + 3 = A(2x + 4) + B
Equating the coefficients ofx, we get
2A = 5 or A = \(\frac { 5 }{ 2 }\)
Equating the constant terms, we get
4A + B = 3 ⇒ B = 3 – 4A
= 3 – \(\frac { 4×5 }{ 2 }\) = – 7
∴ 5x + 3 = \(\frac { 5 }{ 2 }\)(2x + 4) – 7

Question 24.
\(\int { \frac { dx }{ { x }^{ 2 }+2x+2 } equals } \)
(a) xtan^-1(x+1)+c
(b) (x+1)tan^-1x+c
(c) tan^-1(x+1)+c
(d) tan^-1x+c
Solution:
(b) (x+1)tan^-1x+c

Question 25.
\(\int { \frac { dx }{ \sqrt { 9x-{ 4x }^{ 2 } } } equals } \)
(a) \(\frac { 1 }{ 9 } { sin }^{ -1 }\left( \frac { 9x-8 }{ 8 } \right) +c\)
(b) \(\frac { 1 }{ 2 } { sin }^{ -1 }\left( \frac { 8x-9 }{ 9 } \right) +c\)
(c) \(\frac { 1 }{ 3 } { sin }^{ -1 }\left( \frac { 9x-8 }{ 8 } \right) +c\)
(d) \({ sin }^{ -1 }\left( \frac { 9x-8 }{ 9 } \right) +c\)
Solution:

These NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.5 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-7-ex-7-5/

NCERT Solutions for Class 12 Maths Chapter 7 Integrals Exercise 7.5

Exercise 7.5 Class 12 Maths Solutions Question 1.
\(\frac { x }{ (x+1)(x+2) }\)
Solution:
Solution:
let \(\frac { x }{ (x+1)(x+2) }\) ≡ \(\frac { A }{ x+1 } +\frac { B }{ x+2 } \)
∴ x = A(x + 2) + B(x + 1) … (i)
putting x = -1 & x = -2 in (i)
we get A = 1, B = 2
\(\frac{x}{(x+1)(x+2)}=\frac{-1}{x+1}+\frac{2}{x+2}\)
Integrating w.r.t. x, we get
\(\int \frac{x}{(x+1)(x+2)} d x=\int \frac{-1}{x+1} d x+\int \frac{2}{x+2} d x\)
\(\frac{x}{(x+1)(x+2)}=\frac{-1}{x+1}+\frac{2}{x+2}\)
= – log|x + 1| + 2log|x + 2| + C
= – log|x + 1| + log(x + 2)² + C
= log\(\frac{(x+2)^{2}}{|x+1|}\) + C

Ex 7.5 Class 12 NCERT Solutions Question 2.
\(\frac { 1 }{ { x }^{ 2 }-9 } \)
Solution:
Let
\(\frac { 1 }{ { x }^{ 2 }-9 } =\frac { 1 }{ (x-3)(x+3) } \equiv \frac { A }{ x-3 } +\frac { B }{ x+3 } \)
⇒ 1 = A(x + 3) + B(x – 3) … (i)
Put x = 3 in (1), we get 1 = 6B ∴ B = \(\frac { 1 }{ 6 }\)
Put x = – 3 in (1), we get 1 = – 6A ∴ A = \(\frac { – 1 }{ 6 }\)

Question 3.
\(\frac { 3x-1 }{ (x-1)(x-2)(x-3) }\)
Solution:
Let
\(\frac { 3x-1 }{ (x-1)(x-2)(x-3) } =\frac { A }{ x-1 } +\frac { B }{ x-2 } +\frac { C }{ x-3 } \)
∴ 3x – 1 = A(x – 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(- 2) … (i)
Put x = 1 in (1), we get 2 = 2A ∴ A = 1
Put x = 2 in (1), we get 5 = – B ∴ B = – 5
Put x = 3 in (1), we get 8 = 2C ∴ C = 4

Question 4.
\(\frac { x }{ (x-1)(x-2)(x-3) }\)
Solution:
let
\(\frac { x }{ (x-1)(x-2)(x-3) } =\frac { A }{ x-1 } +\frac { B }{ x-2 } +\frac { C }{ x-3 } \)
x = A(x – 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x – 2) … (i)
Put x = 1 in (1), we get 1 = 2A ∴ A = \(\frac { 1 }{ 2 }\)
Put x = 2 in (1), we get 2 = – B ∴ B = – 2
Put x = 3 in (1), we get 3 = 2C ∴ C = \(\frac { 3 }{ 2 }\)

Question 5.
\(\frac { 2x }{ { x }^{ 2 }+3x+2 } \)
Solution:
let
\(\frac { 2x }{ { x }^{ 2 }+3x+2 } =\frac { 2x }{ (x+1)(x+2) } =\frac { A }{ x+1 } +\frac { B }{ x+2 } \)
⇒ 2x = A(x + 2) + B(x + 1) … (i)
put x = -1, -2 in (i)
we get A = -2, B = 4
\(\int \frac{2 x}{(x+1)(x+2)} d x=-2 \int \frac{1}{x+1} d x+4 \int \frac{1}{x+2} d x\)
= – 2log|x + 1| + 4log|x + 2| + C
= 4log|x + 2| – 2log|x + 1| + C

Question 6.
\(\frac { 1-{ x }^{ 2 } }{ x(1-2x) } \)
Solution:

Question 7.
\(\frac { x }{ \left( { x }^{ 2 }+1 \right) \left( x-1 \right) } \)
Solution:
let
\(\frac { x }{ \left( { x }^{ 2 }+1 \right) \left( x-1 \right) } =\frac { A }{ x-1 } +\frac { Bx+C }{ { x }^{ 2 }+1 } \)
⇒ x = A(x² + 1) + (Bx + C)(x – 1) … (1)
Put x = 1 in (1), we get 1 = 2A
∴ A = \(\frac { 1 }{ 2 }\)
Equating the coefficients of x² and constant term, we get A + B = 0 and A – C = 0
∴ B = \(\frac { 1 }{ 2 }\) and C = \(\frac { 1 }{ 2 }\)

Question 8.
\(\frac { x }{ { \left( x-1 \right) }^{ 2 }\left( x+2 \right) } \)
Solution:
\(\frac { x }{ { \left( x-1 \right) }^{ 2 }\left( x+2 \right) } =\frac { A }{ x-1 } +\frac { B }{ { \left( x-1 \right) }^{ 2 } } +\frac { C }{ x+2 } \)
⇒ x = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)² … (i)
Put x = 1 in (1), we get 1 = 3B ∴ B = \(\frac { 1 }{ 3 }\)
Put x = – 2 in (1), we get – 2 = 9C ∴ C = \(\frac { – 2 }{ 9 }\)
Equating the coefficients of x², we get A + C = 0
Hence A = \(\frac { 2 }{ 9 }\)

Question 9.
\(\frac { 3x+5 }{ { x }^{ 3 }-{ x }^{ 2 }-x+1 } \)
Solution:
x³ – x² – x + 1 = x²(x – 1) – 1(x – 1)
= (x² – 1)(x – 1)
= (x + 1) (x – 1) (x – 1)
= (x + 1)(x – 1)²
∴ \(\frac { 3x+5 }{ { x }^{ 3 }-{ x }^{ 2 }-x+1 } \) = \(\frac{3 x+5}{(x+1)(x-1)^{2}}\)
Let \(\frac{3 x+5}{(x+1)(x-1)^{2}}=\frac{\mathrm{A}}{x+1}+\frac{\mathrm{B}}{(x-1)}+\frac{\mathrm{C}}{(x-1)^{2}}\)
3x + 5 = A(x – 1) + B(x – 1)(x + 1) + C (x + 1) … (1)
Put x = – 1 in (1), we get 2 = 4A ∴ A = \(\frac { 1 }{ 2 }\)
Put x = 1 in (1), we get 8 = 2C ∴ C = 4
Equating the coefficients of x², we get A + B = 0
∴ B = \(\frac { -1 }{ 2 }\)

Question 10.
\(\frac { 2x-3 }{ ({ x }^{ 2 }-1)(2x+3) } \)
Solution:
Let \(\frac{2 x-3}{(x-1)(x+1)(2 x+3)}=\frac{\mathrm{A}}{x-1}+\frac{\mathrm{B}}{x+1}+\frac{\mathrm{C}}{2 x+3}\)
2x – 3 = A(x + 1)(2x + 3) + B(x – 1)(2x + 3) + C(x – 1)(x + 1) … (1)
Put x = 1 in (1), we get – 1 = 10A ∴ A = \(\frac { – 1 }{ 10 }\)
Put x = – 1 in (1), we get – 5 = – 2B ∴ B = \(\frac { 5 }{ 2 }\)
Put x = \(\frac { – 3 }{ 2 }\) in (1), we get – 6 = \(\frac { 5 }{ 4 }\)C ∴ C = \(\frac { -24 }{ 5 }\)

Question 11.
\(\frac { 5x }{ (x-1)({ x }^{ 2 }-4) } \)
Solution:
\(\frac { 5x }{ (x-1)({ x }^{ 2 }-4) } =\frac { 5x }{ (x+1)(x+2)(x-2) } \)
Let
\(\frac { 5x }{ (x+1)(x+2)(x-2) }\) = \(\frac{\mathrm{A}}{x+1}+\frac{\mathrm{B}}{x+2}+\frac{\mathrm{C}}{x-2}\)
5x = A(x + 2) (x – 2) + B(x + 1) (x – 2) + C (x + 1) (x + 2) … (1)
Put x = – 1 in (1), we get – 5 = – 3 A ∴ A = \(\frac { 5 }{ 3 }\)
Put x = – 2 in (1), we get – 10 = 4B ∴ B = \(\frac { – 5 }{ 2 }\)
Put x = 2 in (1), we get 10 = 12C ∴ C = \(\frac { 5 }{ 6 }\)

Question 12.
\(\frac { { x }^{ 3 }+x+1 }{ { x }^{ 2 }-1 } \)
Solution:
Degree of Nr > Degree of Dr

Question 13.
\(\frac { 2 }{ (1-x)(1+{ x }^{ 2 }) } \)
Solution:

Question 14.
\(\frac { 3x-1 }{ { (x+2) }^{ 2 } } \)
Solution:
\(\frac { 3x-1 }{ { (x+2) }^{ 2 } } \equiv \frac { A }{ x+1 } +\frac { B }{ { (x+2) }^{ 2 } } \)
∴ 3x – 1 = A(x + 2) + B … (i)
Put x = – 2 in (1), we get – 7 = B ∴B = – 7
Equating the coefficients of x, we get A = 3
∴ \(\frac{3 x-1}{(x+2)^{2}}=\frac{3}{(x+2)}-\frac{7}{(x+2)^{2}}\)
\(\int \frac{3 x-1}{(x+2)^{2}} d x=3 \int \frac{1}{(x+2)} d x-7 \int \frac{1}{(x+2)^{2}} d x\)
= 3 log|x+2| – 7(\(\left(\frac{-1}{x+2}\right)\)) + C
= \(3log|x+2|+\frac { 7 }{ x+2 } +C\)

Question 15.
\(\frac { 1 }{ { x }^{ 4 }-1 } \)
Solution:
\(\frac { 1 }{ { x }^{ 4 }-1 } \)
= \(\frac{1}{\left(x^{2}-1\right)\left(x^{2}+1\right)}\)
= \(\overline{(x-1)(x+1)\left(x^{2}+1\right)}\)
Let
\(\frac { 1 }{ { x }^{ 4 }-1 } =\frac { A }{ x+1 } +\frac { B }{ x-1 } +\frac { Cx+D }{ { x }^{ 2 }+1 } \)
1 = A(x + 1)(x² + 1) + B(x – 1)(x² + 1) + (Cx + D)(x² – 1)
1 = A(x + 1)(x² + 1) + B(x – 1)(x² + 1) + C(x³ – x) + D(x² – 1) … (1)
Put x = 1 in (1), we get 1 = 4A
∴ A = \(\frac { 1 }{ 4 }\)
Put x = -1 in (1), we get 1 = – 4B
∴ B = \(\frac { – 1 }{ 4 }\)
Equating coefficients of x³ and constant terms, we get,
A + B + C = 0
A – B – D = 1
∴ C = 0 and D = \(\frac { – 1 }{ 2 }\)
\(\frac{1}{x^{4}-1}=\frac{1}{4(x-1)}-\frac{1}{4(x+1)}-\frac{1}{2\left(x^{2}+1\right)}\)
Integrating w.r.t. x, we get

Question 16.
\(\frac { 1 }{ x({ x }^{ n }+1) } \)
Solution
Multiply numerator and denominator by x^n-1

Question 17.
\(\frac { cosx }{ (1-sinx)(2-sinx) } \)
Solution:
Put t = sinx, \(\frac { dt }{ dx }\) = cosx, dt = cosx dx

Question 18.
\(\frac { \left( { x }^{ 2 }+1 \right) \left( { x }^{ 2 }+2 \right) }{ \left( { x }^{ 2 }+3 \right) \left( { x }^{ 2 }+4 \right) } \)
Solution:

Question 19.
\(\frac { 2x }{ ({ x }^{ 2 }+1)({ x }^{ 2 }+3) } \)
Solution:
put x² = y
so that 2x dx = dy
\(\int \frac{2 x}{\left(x^{2}+1\right)\left(x^{2}+3\right)} d x=\int \frac{d t}{(t+1)(t+3)}\)
Let \(\frac{1}{(t+1)(t+3)}=\frac{A}{t+1}+\frac{B}{t+3}\)
∴ 1 = A(t + 3) + B(t + 1) … (1)
Put t = – 1 in (1), we get 1 = 2A ∴ A = \(\frac { 1 }{ 2 }\)
Put x = – 3 in (1), we get 1 = – 2B ∴ B = \(\frac { – 1 }{ 2 }\)

Question 20.
\(\frac { 1 }{ x({ x }^{ 4 }-1) } \)
Solution:

Question 21.
\(\frac { 1 }{ { e }^{ x }-1 } \)
Solution:

Question 22.
Choose the correct answer in each of the following :
\(\int { \frac { xdx }{ (x-1)(x-2) } equals } \)
(a) \(log\left| \frac { { (x-1) }^{ 2 } }{ x-2 } \right| + C\)
(b) \(log\left| \frac { { (x-2) }^{ 2 } }{ x-1 } \right| + C\)
(c) \(log\left| \left( \frac { x-{ 1 }^{ 2 } }{ x-2 } \right) \right| +C\)
(d) log|(x – 1)(x – 2)| + C
Solution:
Let \(\frac{x}{(x-1)(x-2)}=\frac{A}{(x-1)}+\frac{B}{(x-2)}\)
∴ x = A(x – 2) + B(x – 1) … (1)
Put x = 1 in (1), we get 1 = – A ∴ A = – 1
Put x = 2 in (1), we get B = 1

Question 23.
\(\int { \frac { dx }{ x({ x }^{ 2 }+1) } } \) equals
(a) \(log|x|-\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+C \)
(b) \(log|x|+\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+C \)
(c) \(-log|x|+\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+C\)
(d) \(\frac { 1 }{ 2 } log|x|+log({ x }^{ 2 }+1)+C \)
Solution:
\(\int { \frac { dx }{ x({ x }^{ 2 }+1) } } \) dx
Let
\(\frac { 1 }{ x\left( { x }^{ 2 }+1 \right) } =\frac { A }{ x } +\frac { Bx+C }{ { x }^{ 2 }+1 } \)
⇒ 1 = A(x² + 1) + (Bx + C)x
Equating the coefficients of x², x and con-stant term, we get A + B = 0, C = 0, A = 1
Solving the equations, we get A = 1, B = – 1, C = 0
\(\frac{1}{x\left(x^{2}+1\right)}=\frac{1}{x}+\frac{-x}{x^{2}+1}\)
\(\int \frac{1}{x\left(x^{2}+1\right)} d x=\int \frac{1}{x} d x-\frac{1}{2} \int \frac{2 x}{x^{2}+1} d x\)
= \(\log |x|-\frac{1}{2} \log \left|x^{2}+1\right|\) + C