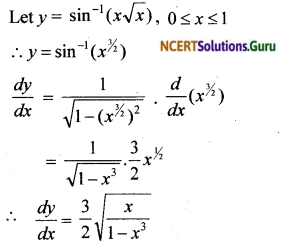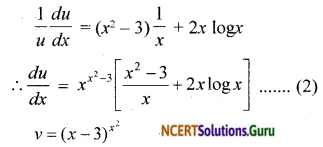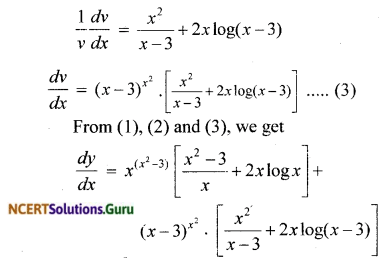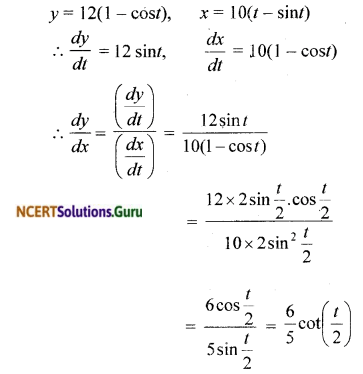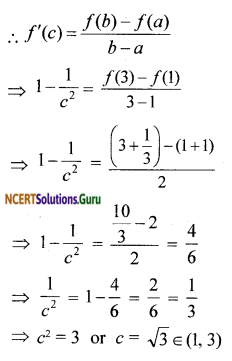CBSE Class 12

These NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.8 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-5-ex-5-8/

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Exercise 5.8

Ex 5.7 Class 12 Maths Ncert Solutions Question 1.
Verify Rolle’s theorem for the function
f(x) = x² + 2x – 8, x ∈ [- 4, 2]
Solution:
Now f(x) = x² + 2x – 8 is a polynomial
∴ It is continuous and derivable in its domain x ∈ R.
Hence it is continuous in the interval [- 4, 2] and derivable in the interval (- 4, 2)
f(-4) = (- 4)² + 2(- 4) – 8 = 16 – 8 – 8 = 0,
f(2) = 2² + 4 – 8 = 8 – 8 = 0
Conditions of Rolle’s theorem are satisfied.
f'(x) = 2x + 2
∴ f’ (c) = 2c + 2 = 0
or c = – 1, c = – 1 ∈ [- 4, 2]
Thus f’ (c) = 0 at c = – 1.

Ex 5.7 Class 12 NCERT Solutions Question 2.
Examine if Rolle’s theorem is applicable to any of the following functions. Can you say some thing about the converse of Rolle’s theorem from these example?
(i) f(x) = [x] for x ∈ [5, 9]
(ii) f (x) = [x] for x ∈ [-2, 2]
(iii) f (x) = x² – 1 for x ∈ [1, 2]
Solution:
(i) In the interval [5, 9], f (x) = [x] is neither continuous nor derivable at x = 6, 7, 8 Hence Rolle’s theorem is not applicable
(ii) f (x) = [x] is not continuous and derivable at – 1, 0, 1. Hence Rolle’s theorem is not applicable.
(iii) f(x) = (x² – 1), f(1) = 1 – 1 = 0,
f(2) = 22 – 1 = 3
f(a) ≠ f(b)
Though it is continous and derivable in the interval [1,2].
Rolle’s theorem is not applicable.
In case of converse if f (c) = 0, c ∈ [a, b] then conditions of rolle’s theorem are not true.
(i) f (x) = [x] is the greatest integer less than or equal to x.
∴ f(x) = 0, But fis neither continuous nor differentiable in the interval [5, 9].

(ii) Here also, theough f (x) = 0, but f is neither continuous nor differentiable in the interval [- 2, 2].

(iii) f (x) = x² – 1, f'(x) = 2x. Here f'(x) is not zero in the [1, 2], So f (2) ≠ f’ (2).

Question 3.
If f: [- 5, 5] → R is a differentiable function and if f (x) does not vanish anywhere then prove that f (- 5) ≠ f (5).
Solution:
For Rolle’s theorem
If (i) f is continuous in [a, b]
(ii) f is derivable in [a, b]
(iii) f (a) = f (b)
then f’ (c) = 0, c ∈ (a, b)
∴ f is continuous and derivable
i.e., f'(c) ≠ 0. Hence \(\frac{f(5)-f(-5)}{10}\)
but f (c) ≠ 0 ⇒ f(a) ≠ f(b)
⇒ f(-5) ≠ f(5)

Question 4.
Verify Mean Value Theorem, if
f (x) = x² – 4x – 3 in the interval [a, b], where a = 1 and b = 4.
Solution:
f (x) = x² – 4x – 3. It being a polynomial it is continuous in the interval [1, 4] and derivable in (1,4), So all the condition of mean value theorem hold.
then f’ (x) = 2x – 4,
f'(c) = 2c – 4
f(4) = 16 – 16 – 3 = – 3,
f(1) = 1 – 4 – 3 = – 6
∴ f'(c) = 0 \(\frac{f(b)-f(a)}{b-a}\) = \(\frac{f(4)-f(1)}{4-1}\)
⇒ 2c – 4 = \(\frac{-3-6}{4-1}\)
⇒ 2c – 4 = 1 ⇒ c = \(\frac{5}{2}\) ∈ (1, 4)
∴ Mean Value Theorem is verified for f(x) on (1, 4)

Question 5.
Verify Mean Value Theorem, if f (x) = x³ – 5x² – 3x in the interval [a, b], where a = 1 and b = 3. Find all c ∈ (1, 3) for which f’ (c) = 0.
Solution:
f (x) = x³ – 5x² – 3x
f'(x) = 3x² – 10x – 3
Since f'(x’) exists, f(x) is continous on [1, 3]
f(x) is differentiable on (1, 3)
f'(c) = 3c² – 10c – 3
f(b) = f(3) = – 27
f(a) = f(1) = – 7
∴ f'(c) = 0 \(\frac{f(b)-f(a)}{b-a}\)
⇒ 3c² – 10c – 3 = \(\frac{-27-7}{3-1}\)
⇒ 3c² – 10c – 3 = – 10
⇒ 3c² – 10c + 7 = 0
⇒ (c – 1)(3c – 7) = 0 ⇒ c = 1 or c = \(\frac{7}{3}\)
\(\frac{7}{3}\) ∈ (1, 3)
∴ Mean Value Theorem is verified for f(x) on (1, 3)

Question 6.
Examine the applicability of Mean Value theroem for all three functions given in the above Question 2.
Solution:
(i) F (x)= [x] for x ∈ [5, 9], f (x) = [x] in the interval [5, 9] is neither continuous, nor differentiable.
(ii) f (x) = [x], for x ∈ [-2, 2],
Again f (x) = [x] in the interval [-2, 2] is neither continous, nor differentiable.
(iii) f(x) = x² – 1 for x ∈ [1,2], It is a polynomial.
Therefore it is continuous in the interval [1,2] and differentiable in the interval (1,2)
f (x) = 2x, f(1) = 1 – 1 = 0 ,
f(2) = 4 – 1 = 3, f'(c) = 2c
∴ f'(c) = 0 \(\frac{f(b)-f(a)}{b-a}\)
2c = \(\frac{3-0}{2-1}\) = \(\frac{3}{1}\)
∴ c = \(\frac{3}{2}\) which belong to (1, 2)

These NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.7 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-5-ex-5-7/

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Exercise 5.7

Ex 5.7 Class 12 Maths Ncert Solutions Question 1.
x² + 3x + 2
Solution:
Let y = x² + 3x + 2
Differentiating both sides w.r.t. x
\(\frac { dy }{ dx }\) = 2x + 3 and \(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \) = 2

Ex 5.7 Class 12 NCERT Solutions Question 2.
x²⁰ = y
Solution:
Let y = x²⁰
Differentiating both sides w.r.t. x
\(\frac { dy }{ dx } ={ 20 }x^{ 19 }\quad ⇒\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =20\times { 19x }^{ 18 }={ 380 }x^{ 18 }\qquad \)

Question 3.
x.cos x = y(say)
Solution:
Let y = x.cos x
Differentiating both sides w.r.t. x
\(\frac { dy }{ dx } \) = x(- sinx) + cosx.1 = – xsinx + cosx
\(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \) = – xcosx – sinx – sinx = – xcosx – 2sinx

Question 4.
log x = y (say)
Solution:
Let y = log x
Differentiating both sides w.r.t. x
\(\frac { dy }{ dx } =\frac { 1 }{ x } ⇒ \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =-\frac { 1 }{ { x }^{ 2 } } \)

Question 5.
x³ log x = y (say)
Solution:
Let y = x³ log x
Differentiating both sides w.r.t. x
\( ⇒\frac { dy }{ dx } ={ x }^{ 3 }.\frac { 1 }{ x } +logx\times { 3x }^{ 2 }={ x }^{ 2 }+{ 3x }^{ 2 }logx \)
\(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =2x+{ 3x }^{ 2 }.\frac { 1 }{ x } +logx.6x=x(5+6logx) \)

Question 6.
e^x sin 5x = y
Solution:

Question 7.
e^6x cos3x
Solution:
Let y = e^6x cos3x
Differentiating both sides w.r.t. x

Question 8.
tan^-1 x
Solution:
Let y = tan^-1 x
Differentiating both sides w.r.t. x
\(\frac { dy }{ dx } =\frac { 1 }{ 1+{ x }^{ 2 } } ⇒\frac { { d }^{ 2y } }{ { dx }^{ 2 } } =\frac { -2x }{ { ({ 1+x }^{ 2 }) }^{ 2 } } \)

Question 9.
log(logx)
Solution:
Let y = log(logx)
Differentiating both sides w.r.t. x

Question 10.
sin(log x)
Solution:
Let y = sin(log x)
Differentiating both sides w.r.t. x

Question 11.
If y = 5 cos x – 3 sin x, prove that \(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } +y=0\)
Solution:
Let y = 5 cos x – 3 sin x
Differentiating both sides w.r.t. x
\(\frac { dy }{ dx } \) = – 5sinx – 3cosx
\(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \) = – 5cosx +3sinx = – y
\(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \) + y = 0
Hence proved

Question 12.
If y = cos^-1 x, Find \(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \) in terms of y alone.
Solution:
Let y = cos^-1 x
Differentiating both sides w.r.t. x
\(\frac { dy }{ dx } = – { \left( { 1-x }^{ 2 } \right) }^{ -\frac { 1 }{ 2 } }\)
\(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =\frac { -cosy }{ { \left( { sin }^{ 2 }y \right) }^{ \frac { 3 }{ 2 } } } = -coty\quad { cosec }^{ 2 }y\)

Question 13.
If y = 3 cos (log x) + 4 sin (log x), show that
\({ x }^{ 2 }{ y }_{ 2 }+{ xy }_{ 1 } \) + y = 0
Solution:
Let y = 3 cos (log x) + 4 sin (log x)
Differentiating both sides w.r.t. x

Question 14.
If A = Ae^mx + Be^nx, show that \(\frac{d^{2} y}{d x^{2}}-(m+n) \frac{d y}{d x}+m n y\) = 0
Solution:
Let y = Ae^mx + Be^nx
Differentiating both sides w.r.t. x
\(\frac { d }{ dx }\) = Ae^mx + Be^nx
Differentiating both sides w.r.t. x
\(\frac{d^{2} y}{d x^{2}}\) = Ae^mx(m) + Be^nx(n)
\(\frac{d^{2} y}{d x^{2}}-(m+n) \frac{d y}{d x}+m n y\)
= Ae^mx . (m²) + Be^nx(n²) – (m + n) [Ae^mx(m) + Be^nx(n)] + mny
= Am²e^mx + Bn²e^nx – [Am²e^mx – Bn²e^nx +mny
= – mn[Ae^mx + Be^nx] + mny
= – mny + mny = 0 = RHS

Question 15.
If y = 500e^7x + 600e^-7x, show that \(\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } \) = 49y.
Solution:
Let y = 500e^7x + 600e^-7x
Differentiating both sides w.r.t. x

Question 16.
If e^y(x+1) = 1, show that \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\)
Solution:
Let y = e^y(x+1)
Differentiating both sides w.r.t. x

Question 17.
If y = (tan^-1 x)² show that (x² + 1)²y₂ + 2x(x² + 1)y₁ = 2
Solution:
Let y = (tan^-1 x)²
Differentiating both sides w.r.t. x

These NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-5-miscellaneous-exercise/

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Question 1.
(3x² -9x + 5)⁹
Solution:
Let y = (3x² -9x + 5)⁹
∴ \(\frac { dy }{ dx }\) = (3x² -9x + 5)⁸. \(\frac { d }{ dx }\)(3x² -9x + 5)
= 9(3x² -9x + 5)⁸ (6x – 9)
= 27 (3x² -9x + 5)⁸ (2x – 3)

Question 2.
sin³x + cos⁶ x
SoL
Let y = sin³x + cos⁶ x
∴ \(\frac { dy }{ dx }\) = 3 sin²x . cosx + 6cos5x (- sinx)
= 3 sinx cosx (sinx – 2 cos⁴x)

Question 3.
(5x)^3cos2x
Solution:
Let y = (5x)^3cos2x
Taking logarithmon both sides,
∴ log y = 3 cos 2x log 5x
Differentiating both sides, w.r.t. x,

Question 4.
sin^-1 (x\(\sqrt{x}\)), 0 ≤ x ≤ 1
Solution:

Question 5.
\(\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}},-2<x<2\)
Solution:

Question 6.
\(\cot ^{-1}\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right], 0<x<\frac{\pi}{2}\)
Solution:

Question 7. \((\log x)^{\log x}, x>1\)
Solution:
Let y = \((\log x)^{\log x}\)
Taking logarithmon both sides,
∴ log y = log x(log log x)
Differentiating both sides, w.r.t. x,
\(\frac { 1 }{ y }\) \(\frac { dy }{ dx }\) = logx.\(\frac { 1 }{ log x }\).\(\frac { 1 }{ x }\) + \(\frac { 1 }{ x }\).log log x
∴ \(\frac { dy }{ dx }\) = (log x)^{log x} [\(\frac { 1 }{ x }\) + \(\frac { log log.x }{ x }\)]

Question 8.
cos (a cos x + b sin x), for sorne constant a and b.
Solution:
Let y = cos (a cosx + b sinx)
\(\frac { dy }{ dx }\) = sin (a cosx + h sinx).
\(\frac { dy }{ dx }\)(a cosx + b sinx)
= – sin (a cosx + b sinx) [- a sinx + b cosx]
= (a sinx – b cosx).sin (a cosx + b sinx)

Question 9.
(sin x – cos x)^{sin x-cos x}, \(\frac { π }{ 4 }\)< x < \(\frac { 3π }{ 4 }\)
Solution:
When \(\frac { π }{ 4 }\)< x < \(\frac { 3π }{ 4 }\), then sin x > cos x
so that sin x – cos x is positive.
Let y = (sinx – cosx)^{sin x-cos x}
Taking logarithm on both sides,
∴ logy = (sinx – cosx) log (sinx – cosx)
Differentiating both sides w.r.t. x,
\(\frac { 1 }{ y }\) \(\frac { dy }{ dx }\)
=( sinx – cosx)\(\frac { 1 }{ sin x-cosx }\) .\(\frac { d }{ dx }\)(sinx-cosx) + log (sinx – cosx). (cosx + sinx)
= (cosx + sinx) + log (sinx – cosx) . (cosx + sinx)
= (cosx + sinx) [1 + log (sinx – cosx)]
∴ \(\frac { dy }{ dx }\) = (sin x – cos x)^{sin x-cos x}(cosx + sinx) [1 + log(sinx – cosx)]

Question 10.
x^x + x^a + a^x + a^a for some fixed a > 0 and x > 0.
Solution:

Question 11.
\(x^{x^{2}-3}+(x-3)^{x^{2}}\), for x > 3
Solution:
Let u = x\(x^{x^{2}-3}\) and v = (x – 3)^x²
Differentiating w.r.t. x,
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\) … (1)
u = x^x²-3
Taking logarithm on bath sides,
∴ log u = (x² – 3)log
Differentiating both sides w.r.t. x,

Taking logarithm on bath sides,
∴ log v = x²log(x – 3)
Differentiating both sides w.r.t. x,

Question 12.
Find \(\frac { dy }{ dx }\), if y = 12(1 – cos t),
x = 10(t – sin t), \(\frac { – π }{ 2 }\) < t < \(\frac { π }{ 2 }\)
Solution:

Question 13.
Find \(\frac { dy }{ dx }\), if
y = sin^-1 x + sin^-1 \(\sqrt{1-x^{2}},-1 \leq x \leq 1\).
Solution:

Question 14.
If \(x \sqrt{1+y}+y \sqrt{1+x}\) = 0, for – 1 < x < 1, prove that \(\frac { dy }{ dx }\) = – \(\frac{1}{(1+x)^{2}}\)
Solution:
\(x \sqrt{1+y}+y \sqrt{1+x}\) = 0
\(x \sqrt{1+y}\) = – y\(\sqrt{1+y}\)
Squaring both sides,
x²(1 + y) = y²(1 + x)
x² + x²y = y² + y²x
x² – y² = y²x – x²y
(x – y)(x + y) = xy(x – y)
(x + y) = – xy
y + xy = – x
y(1 + x) = – x
∴ y = \(\frac { – x }{ 1+x }\)
Differentiating w.r.t. x,
\(\frac { dy }{ dx }\) = \(\frac{(1+x)(-1)-(-x) 1}{(1+x)^{2}}\)
= \(\frac{-1-x+x}{(1+x)^{2}}\) = \(\frac{-1}{(1+x)^{2}}\), x ≠ – 1

Question 15.
If (x – a)² + (y – b)² = c², for some c > 0, prove that
\(\frac{\left[1+\left(\frac{d y}{d x}\right)^{2}\right]^{\frac{3}{2}}}{\frac{d^{2} y}{d x^{2}}}\)
is a constant, independent of a and b.
Solution:

Question 16.
If cos y = x cos (a + y), with
cos a ≠ ± 1, prove that \(\frac { dy }{ dx }\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\)
Solution:

Question 17.
If x = a(cos t + t sin t) and y = a(sin t – t cos t), find \(\frac{d^{2} y}{d x^{2}}\)
Solution:

Question 18.
If f(x) = |x|³, show that f”(x) exists for all real x and find it.
Solution:
f(x) can be redefined as
f(x) = \(\left\{\begin{aligned}
x^{3}, & x \geq 0 \\
-x^{3}, & x<0 \end{aligned}\right.\) For x > 0 and x < 0, fix) is a polynomial function. Hence f(x) is differentiable for x > 0 and x < 0. ∴ For x > 0, f'(x) = 3x² and f”(x) = 6x
For x < 0, f'(x) = – 3x² and f”(x) = – 6x

or f”(x) = 6|x| exists for all x ∈ R

Question 19.
Using mathematical induction, prove that \(\frac { d }{ dx }\)(xⁿ) = \(n x^{n^{-1}}\) for all positive integers n.
Solution:

Hence P(k + 1) is true.
i.e., P(k + 1) is true whenever P(k) is true.
Hence by the principle of mathematical induction, \(\frac { d }{ dx }\)(xⁿ) = nx^n-1 is true for positive integer n.

Question 20.
Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines.
Solution:
sin (A + B) = sin A cos B + cos A sin B
Differentiating both sides w.r.t. x,

Question 21.
Does there exist a function which is continuous everywhere but not differentiable at exactly two points? Justify your answer.
Solution:
Yes.
i. Let f(x) = |x – 1| + |x – 2|
Let g(x) = |x|, h(x) = x – 1, k(x) = x – 2.
Then g(x), h(x) and k(x) are continuous functions since h(x) and k(x) are polynomial functions and g(x) ¡s the modulus function.

at x = 1, since Lf’(1) ≠ Rf’(1)
Similarly we can show that f(x) ¡s not differentiable at x = 2.
Thus f(x) = |x – 1| + |x – 2| is continuous everywhere and not differentiable at exactly two points, namely at x = 1 or x = 2.

Question 22.
If y = \(\left|\begin{array}{ccc}
f(x) & g(x) & h(x) \\
l & m & n \\
a & b & c
\end{array}\right|\), prove that \(\frac { dy }{ dx }\) = \(\left|\begin{array}{ccc}
f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\
l & m & n \\
a & b & c
\end{array}\right|\)
Solution:

Question 23.
If y = \(e^{a \cos ^{-1} x}\), – 1 ≤ x ≤ 1, show that (1 – x²)\(\frac{d^{2} y}{d x^{2}}-x \frac{d y}{d x}-a^{2} y\) = 0
Solution:
f(x) = x + \(\frac { 1 }{ x }\)
f(x) is a continuous function in [1, 3]
Ax) is differentiable in(1,3)
f’(x) = 1 + \(\\frac{-1}{x^{2}}\) exists for x ∈ (1, 3)

These NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.4 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-5-ex-5-4/

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Exercise 5.4

Ex 5.4 Class 12 NCERT Solutions Question 1.
\(\frac { { e }^{ x } }{ sinx } \)
Solution:
\(y=\frac { { e }^{ x } }{ sinx } \)
\(for\quad y=\frac { u }{ v } ,\)
\(\frac { dy }{ dx } =\frac { { e }^{ x }{ sin }x-{ e }^{ x }cosx }{ { sin }^{ 2 }x } \)
\(or\frac { dy }{ dx } =\frac { { e }^{ x }{ sin }x-{ e }^{ x }cosx }{ { sin }^{ 2 }x } ,where\quad x\neq n\pi ,x\in z \)

Exercise 5.4 Class 12 Maths NCERT Solutions Question 2.
\({ e }^{ { sin }^{ -1 }x }\)
Solution:

Question 3.
\({ e }^{ { x }^{ 3 } }\) = y
Solution:
Let y = \({ e }^{ { x }^{ 3 } }\)
Differentiating w.r.t. x,
\(\frac{d y}{d x}=\frac{d}{d x}\left(e^{x^{3}}\right)\) = \(e^{x^{3}} \cdot \frac{d}{d x}\left(x^{3}\right)\)
= \({ e }^{ { x }^{ 3 } }\).3x² = 3x²\({ e }^{ { x }^{ 3 } }\)

Question 4.
\(sin\left( { tan }^{ -1 }{ e }^{ -x } \right)\) = y
Solution:
\(sin\left( { tan }^{ -1 }{ e }^{ -x } \right)\) = y
\(\frac { dy }{ dx } =cos\left( { tan }^{ -1 }{ e }^{ -x } \right) \frac { d }{ dx } \left( { tan }^{ -1 }{ e }^{ -x } \right) \)
\(=cos\left( { tan }^{ -1 }{ e }^{ -x } \right) \frac { 1 }{ 1+{ e }^{ -2x } } \frac { d }{ dx } \left( { e }^{ -x } \right) \)
\(=-cos\left( { tan }^{ -1 }{ e }^{ -x } \right) \frac { 1 }{ 1+{ e }^{ -2x } } .\left( { e }^{ -x } \right) \)

Question 5.
\(log(cos\quad { e }^{ x })\) = y
Solution:
\(\frac { dy }{ dx } =\frac { 1 }{ cos\quad { e }^{ x } } \left( -sin{ e }^{ x } \right) .{ e }^{ x }\quad =-tan\left( { e }^{ x } \right) \)

Question 6.
\({ e }^{ x }+{ e }^{ { x }^{ 2 } }+\)…\(+{ e }^{ { x }^{ 5 } }\) = y(say)
Solution:

Question 7.
\(\sqrt { { e }^{ \sqrt { x } } }\), x > 0
Solution:

Question 8.
log(log x), x > 1
Solution:
y = log(log x), x > 1
Differentiating w.r.t. x,
\(\frac{d y}{d x}\) = \(\frac{1}{\log x} \cdot \frac{d}{d x}\)(log x)
= \(\frac{1}{\log x} \cdot \frac{1}{x}\) = \(\frac{1}{x \log x}\), x > 1

Question 9.
\(\frac { cosx }{ logx }\) = y(say),x>0
Solution:

Question 10.
cos(log x + ex), x > 0
Solution:

These NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.3 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-5-ex-5-3/

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Exercise 5.3

Ex 5.3 Class 12 NCERT Solutions Question 1.
2x + 3y = sinx
Solution:
2x + 3y = sinx
Differentiating w.r.t x,
\(2+3\frac { dy }{ dx } =cosx \)
⇒ \(\frac { dy }{ dx } =\frac { 1 }{ 3 } (cosx-2)\)

Exercise 5.3 Class 12 Maths Ncert Solutions In Hindi Question 2.
2x + 3y = siny
Solution:
2x + 3y = siny
Differentiating w.r.t x,
\(2+3.\frac { dy }{ dx } =cosy\frac { dy }{ dx } \)
⇒ \(\frac { dy }{ dx } =\frac { 2 }{ cosy-3 } \)

Question 3.
ax + by² = cosy
Solution:
ax + by² = cosy
Differentiate both sides w.r.t. x,

Question 4.
xy + y² = tan x + y
Solution:
xy + y² = tan x + y
Differentiate both sides w.r.t. x,

Question 5.
x² + xy + y² = 100
Solution:
x² + xy + y² = 100
Differentiate both sides w.r.t. x,

Question 6.
x³ + x²y + xy² + y³ = 81
Solution:
x³ + x²y + xy² + y³ = 81
Differentiate both sides w.r.t. x,

Question 7.
sin² y + cos xy = π
Solution:
sin² y + cos xy = π
Differentiate both sides w.r.t. x,

Question 8.
sin²x + cos²y = 1
Solution:
Given that
sin²x + cos²y = 1
Differentiating both sides, we get

Question 9.
y = \({ sin }^{ -1 }\left( \frac { 2x }{ { 1+x }^{ 2 } } \right)\)
Solution:

Question 10.
y = \({ tan }^{ -1 }\left( \frac { { 3x-x }^{ 3 } }{ { 1-3x }^{ 2 } } \right) ,-\frac { 1 }{ \sqrt { 3 } } <x<\frac { 1 }{ \sqrt { 3 } } \)
Solution:

Question 11.
y = \({ cos }^{ -1 }\left( \frac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } } \right) ,0<x<1\)
Solution:
y = \({ cos }^{ -1 }\left( \frac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } } \right) ,0<x<1\)
put x = tanθ
y = \({ cos }^{ -1 }\left( \frac { 1-tan^{ 2 }\quad \theta }{ 1+{ tan }^{ 2 }\quad \theta } \right) ={ cos }^{ -1 }(cos2\theta )=2\theta\)
= 2θ = 2 tan^{-1 x}
i.e., y = 2 tan^-1x
Differentiating w.r.t x, \(\frac{d y}{d x}=\frac{2}{1+x^{2}}\)

Question 12.
y = \({ sin }^{ -1 }\left( \frac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } } \right) ,0<x<1\)
Solution:

Question 13.
y = \({ cos }^{ -1 }\left( \frac { 2x }{ 1+{ x }^{ 2 } } \right)\), – 1 < x < 1
Solution:

Question 14.
y = \(sin^{ -1 }\left( 2x\sqrt { 1-{ x }^{ 2 } } \right) ,-\frac { 1 }{ \sqrt { 2 } } <x<\frac { 1 }{ \sqrt { 2 } } \)
Solution:

Question 15.
y = \(sin^{ -1 }\left( \frac { 1 }{ { 2x }^{ 2 }-1 } \right) ,0<x<\frac { 1 }{ \sqrt { 2 } } \)
Solution:
y = \(sin^{ -1 }\left( \frac { 1 }{ { 2x }^{ 2 }-1 } \right) ,0<x<\frac { 1 }{ \sqrt { 2 } } \)
put x = tanθ
we get
y = \(sec^{ -1 }\left( \frac { 1 }{ { 2cos }^{ 2 }\theta -1 } \right) ={ sec }^{ -1 }\left( \frac { 1 }{ cos2\theta } \right) \)
y = \(sec^{ -1 }(sec2\theta )=2\theta ,\quad 2{ cos }^{ -1 }x \)
i.e., y = 2 cos^-1 x
Differentiating w.r.t.x,
∴ \(\frac{d y}{d x}=\frac{-2}{\sqrt{1-x^{2}}}\)

These NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.2 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-5-ex-5-2/

NCERT Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Exercise 5.2

Class 12 Maths Chapter 5 Exercise 5.2 Question 1.
sin(x² + 5)
Solution:
Let y = sin(x² + 5),
put x² + 5 = t
y = sint
t = x²+5
\(\frac { dy }{ dx } =\frac { dy }{ dt } .\frac { dt }{ dx } \)
\(\frac { dy }{ dx } =cost.\frac { dt }{ dx } =cos({ x }^{ 2 }+5)\frac { d }{ dx } ({ x }^{ 2 }+5)\)
= cos (x² + 5) × 2x
= 2x cos (x² + 5)

Ex 5.2 Class 12 NCERT Solutions Question 2.
cos (sin x)
Solution:
let y = cos (sin x)
put sinx = t
∴ y = cost,
t = sinx
∴\(\frac { dy }{ dx } =-sin\quad t,\frac { dt }{ dx } =cos\quad x \)
\(\frac { dy }{ dx } =\frac { dy }{ dt } .\frac { dt }{ dx } =(-sint)\times cosx\)
Putting the value of t, \(\frac { dy }{ dx } =-sin(sinx)\times cosx\)
\(\frac { dy }{ dx } =-[sin(sinx)]cosx\)

Ncert Solutions For Class 12 Maths Chapter 5 Exercise 5.2 Question 3.
sin(ax+b)
Solution:
let = sin(ax+b)
put ax+bx = t
∴ y = sint
t = ax+b
\(\frac { dy }{ dt } =cost,\frac { dt }{ dx } =\frac { d }{ dx } (ax+b)=a\)
\(Now\frac { dy }{ dx } =\frac { dy }{ dt } .\frac { dt }{ dx } =cost\times a=acos\quad t\)
\(\frac { dy }{ dx } =acos(ax+b)\)

Exercise 5.2 Class 12 NCERT Solutions Question 4.
sec(tan(\(\sqrt{x}\)))
Solution:
let y = sec(tan(\(\sqrt{x}\)))
by chain rule
\(\frac { dy }{ dx } =sec(tan\sqrt { x } )tan(tan\sqrt { x } )\frac { d }{ dx } (tan\sqrt { x } )\)
\(\frac { dy }{ dx } =sec(tan\sqrt { x } ).tan(tan\sqrt { x } ){ sec }^{ 2 }\sqrt { x } .\frac { 1 }{ 2\sqrt { x } } \)

Question 5.
\(\\ \frac { sin(ax+b) }{ cos(cx+d) } \)
Solution:

Question 6.
cos x³ . sin²(x⁵) = y(say)
Solution:
Let y = cos x³ . sin²(x⁵)

Question 7.
\(2\sqrt { cot({ x }^{ 2 }) }\)
Solution:

Question 8.
cos(\(\sqrt{x}\))
Solution:

Question 9.
Prove that the function f given by f (x) = |x – 1|, x ∈ R is not differential at x = 1.
Solution:

∴ f is not differentiable at x = 1

Question 10.
Prove that the greatest integer function defined by f (x) = [x], 0 < x < 3 is not differential at x = 1 and x = 2.
Solution:

Hence f is not differentiable at x = 2