Here you will find Coordinate Geometry Class 10 Extra Questions Maths Chapter 7 with Answers Solutions, Extra Questions for Class 10 Maths are solved by experts and will guide students in the right direction.
Extra Questions for Class 10 Maths Coordinate Geometry with Answers Solutions
Extra Questions for Class 10 Maths Chapter 7 Coordinate Geometry with Solutions Answers
Coordinate Geometry Class 10 Extra Questions Objective Type
Question 1.
The point (-13, -14) lies in :
(a) 1st quadrant
(b) 2nd quadrant
(c) 3rd quadrant
(d) None of these.
Answer:
(c) 3rd quadrant
Question 2.
Point (8, -8) is in which quadrant?
(a) First
(b) Second
(c) Third
(d) Fourth.
Answer:
(d) Fourth.
Question 3.
The position of the point with abscissa = -5 and ordinate = +4 will be :
(a) In the first quadrant
(b) In the second quadrant
(c) In the third quadrant
(d) None of these.
Answer:
(b) In the second quadrant
![]()
Question 4.
Distance of point (-6, 8) from origin is :
(a) 8
(b) 2√7
(c) 10
(d) 6
Answer:
(c) 10
Solution.
Distance of point (-6, 8) from origin (0, 0) is

∴ Choice (c) is correct.
Question 5.
Coordinates of a point on X-axis which is equal distance from the points A(2, -5) and B(-2, 9) will be :
(a) (-7, 0)
(b)(0, 7)
(c) 0, -7)
(d) (7, 0).
Answer:
(a) (-7, 0)
Solution.
Any point on X-axis is P(x, 0)
∴ AP = BP ⇒ AP2 = BP2
= (x – 2)2 + (-5 – 0)2 = (x + 2)2 + (9 – 0)2
= x2 – 4x + 4 + 25 = x2 + 4x + 4 + 81
x2 – 4x + 29 = x2 + 4x + 85
– 8x = 85 – 29 = 56
x = \(\frac{56}{-8}\) = -7
∴ point P on x – axis is (-7, 0)
Hence choice (a) is correct.
Question 6.
The coordinate of a point on Y-axis which is equidistant from the point A(6, 5) and B(-4, 3) will be :
(a) (0, 9)
(b) (0, -9)
(c) (0, 5)
(d) (0, 3)
Answer:
(a) (0, 9
Solution.
Let point P is on Y-axis whose coordinate is (0, y)
PA = PB
⇒ PA2 = PB2
(6 – 0)2 + (5 – y)2 = (-4 -0)2 + (3 – y)2
⇒ 36 + 25 + y2 – 10y = 16 + 9 + y2 – 6y
⇒ 61 – 10y = 25 – 6y
⇒ 61 – 25 = – 6y + 10y
⇒ 4y = 36
⇒ y = 9
Required point P(0, 9)
Hence choice (a) is correct. (a)
Question 7.
A point lies in third quadrant. Co-ordinates of this point may be :
(a) (5, 5)
(b) (5, -5)
(c) (-5, -5)
(d) (-5, 5).
Answer:
(c) (-5, -5)
Question 8.
The distance between the points (5, – 3) and (8, 1) is:
(a) 5 units
(b) 6 units
(c) 25 units
(d) 10 units.
Answer:
(a) 5 units
![]()
Question 9.
The distance between the points (2, 0) and (-1, 4) is :
(a) 5 units
(b) 25 units
(c)- 25 units
(d) 10 units.
Answer:
(a) 5 units
Question 10.
The distance between the points (-6, 5) and (-1, 7) is :
(a) 169 units
(b) √119 units
(c) √13 units
(d) None of these.
Answer:
(d) None of these.
Question 11.
The co-ordinates of a point Mare (3, 4). Its distance from the origin is :
(a) 7 units
(b) 11 units
(c) 5 units
(d) 12 units.
Answer:
(c) 5 units
Question 12.
The distance between points (7, 3) and (-5, -2) is :
(a) 10 units
(b) 13 units
(c) 16 units
(d) 18 units.
Answer:
(b) 13 units
Question 13.
The distance between origin and (15, 8) is :
(a) 18 units
(b) 15 units
(c) 17 units
(d) 28 units.
Answer:
(c) 17 units
Question 14.
The distance between (-1, -3) and (3, 0) is :
(a) 4 units
(b) 5 units
(c) 13 units
(d) 16 units.
Answer:
(b) 5 units
![]()
Question 15.
The distance between the points (-3, 4) and (0, 0) will be :
(a) 5
(b) 4
(c) 13
(d) 1
Answer:
(a) 5
Question 16.
The third vertex of an equilateral triangle whose other two vertices are (1, 1) and (1, -1) respectively is :
(a) (√3, – √3)
(b) (- √3, √3)
(c) both (a) and (b)
(d) none of these.
Answer:
(c) both (a) and (b)
Question 17.
The coordinates of two points are (6, 0) and (0, 8). The coordinates of the mid-point are :
(a) (3, 4)
(b) (6, 8)
(c) (0, 0)
(d) None of these.
Answer:
(a) (3, 4)
Question 18.
The co-ordinates of two points are (9, 4) and (3, 8). The co-ordinates of the mid-point are :
(a) (6, 0)
(b) (0, 6)
(c) (6, 6)
(d) (-6, -6).
Answer:
(c) (6, 6)
![]()
Question 19.
The co-ordinates of two points are (-8, 0) and (0, -8). The co-ordinates of the midpoint of the line segment joining them will be :
(a) (-8, 4)
(b) (4, -8)
(c) (-4, -4)
(d) (-4, 4)
Answer:
(c) (-4, -4)
Question 20.
The abscissa of the point which divides the line joining points (0, 4) and (0, 8) internally in the ratio of 3 : 1 will be :
(a) 0
(b) 4
(c) 6
(d) 5
Answer:
(a) 0
Coordinate Geometry Class 10 Extra Questions Very Short Answer Type
Question 1.
Find the coordinate of a point A. Where AB is the diameter of a circle whose centre is (2, -3) and coordinate of B is (1, 4).
Solution.
As centre is the mid point of AB.

Let coordinate of A is (x, y)
∴ \(\frac{x+1}{2}\) = 2
⇒ 2 x + 1 = 4
⇒ x = 4 – 1 = 3
and \(\frac{y+4}{2}\) = -3 = y + 4 = -6
y = – 10
Hence coordinate of A is (3, -10)
![]()
Question 2.
What are the ordinate of the point whose abscissa is 10 and whose distance from (2, -3) is 10 units?
Solution.
Let y be the ordinate, then the point is (10, y). The distance between (10, y) and (2, -3)
![]()
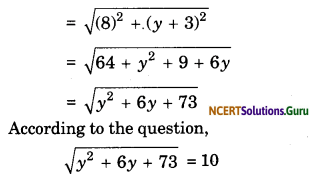
⇒ y2 + 6y + 73 = 100
⇒ y2 + 6y – 27 = 0
⇒ (y +9)(y – 3) = 0
⇒ y = -9, y = 3.
Question 3.
Find the distance between the points A(a sin θ, a cos θ) and B(a cos θ, – a sin θ).
Solution.
Here x1 = a sin θ, x2 = a cos θ y1 = a cos θ, y2 = – a sin AB
Distance AB

Question 4.
Prove that the point (4, 1) is the centre of the circle on whose circumference lie the points (-2, 9), (10, -7) and (12, -5).
Solution.
Let A(-2, 9), B(10, -7), C(12, – 5) and O(4, 1). Then,
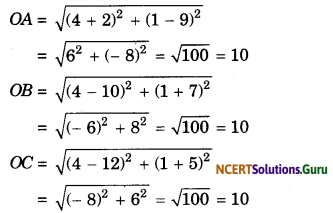
∴ OA = OB = 0C.
Hence O is the centre and A, B, C are the points on the circumference of the circle.
![]()
Question 5.
Find that ratio in which the point \(P\left(\frac{3}{4}, \frac{5}{12}\right)\) divides the line segment joining the points \(A\left(\frac{1}{2}, \frac{3}{2}\right)\) and B(2, -5).
Solution.
Let P divides AB in the ratio λ : 1

⇒ 3λ + 3 = 8λ + 2
⇒ 5λ = 1
λ = \(\frac {1}{5}\)
Hence P divides AB in ratio 1 : 5
Question 6.
Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B.
Solution.
Let M (0, 0) and N (36, 15) be the given points.
Here, x1 = 0, y1 = 0 and x2 = 36, y2 = 15

Since, the position of towns A and B are given (0, 0) and (36, 15), respectively and so, the distance between them is 39 km.
Question 7.
Find the coordinates of that point which divides the line segment joining two given points (3, 5) and (8, 10) internally in the ratio of 2 : 3.
Solution.
Here, x1 = 3, x2 = 8, y1 = 5, y2 = 10, m = 2, n = 3.

![]()
Hence, the co-ordinates of the required point are (5, 7).
![]()
Question 8.
If the area of ∆ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove x + y = 15.
Solution.
Area of ∆ = \(\frac{1}{2}\) [x1 (y2 – y3) + x2(y3 – y1)+ x3 y1 – y2)]
⇒ 6 = \(\frac{1}{2}\)[x(2 – 1) + 1(1 – y) + 2 (y – 2)]
⇒ 12 = x – y + 1 + 2y – 4
⇒ 12 = x + y = 3
∴ x + y = 15
Question 9.
Find the coordinates of point which divide line segment AB joining points A(-2, 2) and B( 2, 8) into four equal parts.
Solution.
Clearly point a is the midpoint of AB

Question 10.
The coordinates of one endpoint of a diameter of a circle are (3, 5). If the coordinates of the centre be (6, 6), find the coordinates of the other endpoint of the diameter.
Solution.
Let AB be the given diameter and O the centre of the circle. Then, the coordinates of A and O and (3, 5) and (6, 6) respectively. Let (a, b) be the coordinates of B.
Then \(\frac{3+a}{2}\) = 6 and \(\frac{5+b}{2}\) = 6
∴ a = 9 and 6 = 7.
Hence, the required point is (9, 7).
![]()
Question 11.
If the points (6, 9),(0, x)and (-6, -7) are collinear then find the value of x.
Solution.
x1 = 6, y1 = 9
x2 = 0, y2 = x
x3 = -6, y3 = -7
The three points are collinear if the area of the triangle formed by them is zero.
Now,
area = \(\frac{1}{2}\)[x1(y2 – y3) + x2(y3 – y1)
+ x3(y1 – y2)] = 0
⇒ \(\frac{1}{2}\)[6(x + 7) + 0(-7 – 9) + (-6)(9 – x)) = 0
⇒ 6x + 42 – 54 + 6x = 0
⇒ 12x = 12
⇒ x = 1.
Question 12.
Find the value of the points (a, 1), (1, -1) and (11, 4) are collinear.
Solution.
Here, A(a, 1) = (x1, y1) B(1, -1) = (x2, y2,) andC(11, 4) = (x3, y3)
Condition for collinear points
⇒ x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)
⇒ a(-1 -4) + 1(4 – 1) + 11(1 + 1) = 0
⇒ -5a + 3 + 22 = 0
⇒ -5a = -25
⇒ a = 5
∴ The given three points are collinear.
Coordinate Geometry Class 10 Extra Questions Short Answer Type
Question 1.
Show that the points (2, 1),(5, 2), (6, 4) and (3, 3) form a parallelogram.
Solution.
Let A(2, 1), B(5, 2), C(6, 4) and D(3, 3).


Thus, AB = CD, BC = DA.
Since, opposite sides are equal, hence ABCD is a parallelogram.
![]()
Question 2.
Prove that the points A(1, -2), B(3, 0) and C(1, 2) are the vertices of an isosceles right-angled triangle.
Solution.
Let A = (1, -2), B = (3, 0) and C = (1, 2).

CA = 4
Now, AB2 + BC2 = (2√2)2 + (2√2)2
= 8 + 8 = 16
AB2 + BC2 = (AC)2 …(4)
Hence, from result (1), (2) and (4) ∆ABC is an isosceles right-angled triangle.
Question 3.
Find the centre of the circle which passes through the points (-3, -2), (-2, 3) and (3, 2).
Solution.
Let O(x, y) be the centre of the circle and the points
A(-3, – 2), B(-2, 3) and C(3, 2)
lie on the circle, Then, we have
OA2 = (x + 3)2 + (y + 2)2
OB2 = (x + 2)2 + (y – 3)2
and OC2 = (x – 3)2 + (y – 2)2
∵ OA = OB
⇒ OA2 = OB2
∴(x + 3)2 + (y + 2)2 = (x + 2)2 + (y – 3)2
⇒ x2 + y2 + 6x + 4y + 13
= x2 + y2 + 4x – 6y + 13
⇒ 6x + 4y = 4x – 6y
⇒ 2x + 10y = 0
⇒ x + 5y = 0 ……(i)
Again, OB = OC
⇒ OB2 = OC2
∴ (x + 2)2 + (y – 3)2 = (x – 3)2 + (y – 2)2
⇒ x2 + y2 + 4x – 6y + 13
= x2 + y2 – 6x – 4y + 13
⇒ 4x – 6y = – 6x – 4y
⇒ 10x – 2y = 0
⇒ 5x – y = 0 …..(ii)
On solving (i) and (ii), we get
x = 0 and y = 0.
Hence, the centre of the circle is (0, 0).
![]()
Question 4.
Prove that the triangle whose vertices are respectively (a, a), (-a, -a) and (-a√3, a√3) is an equilateral triangle.
Solution.
Let points P(a, a), Q(-a, -a) and R(-a√3, a√3) are given, then
and
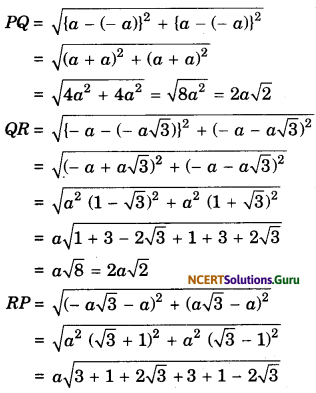
= a√8 = 2a√2
Thus, PQ = QR = RP
∴ ∆PQR is an equilateral triangle.
Question 5.
Find the point on the X-axis which is equidistant from (2, -5) and (-2, 9).
Solution.
Since, the point on the X-axis.
∴ it’s ordinate = 0
So, A(x, 0) is any point on the X-axis.
Since, A(x, 0) is equidistant from B(2, -5) and C(-2, 9).
AB = AC
⇒ AB2 = AC2
⇒ (x – 2)2 + (0 + 5)2 = (x + 2)2 + (0 – 9)2
![]()
⇒ x2 – 4x + 4 + 25 = x2 + 4x + 4 + 81
⇒ -4x – 4x = 81 – 25
⇒ -8x = 56
⇒ x = –\(\frac{56}{8}\) = -7
So, the point equidistant from given points on the x-asis is (-7, 0).
![]()
Question 6.
Find the values of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
Solution.
According to question,
PQ = 10
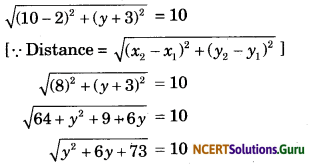
Squaring both sides, we get
⇒ y2 + 6y + 73 = 100
⇒ y2 + 6y – 27 = 0
⇒ y2 + 9y – 3y – 27 = 0
⇒ y(y + 9) – 3 (y + 9) = 0
⇒ (y + 9) (y – 3) = 0
⇒ y = -9 or y = 3
⇒ y = -9 or 3
Question 7.
Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).
Solution.
Let the point A(x, y) be equidistant from the points B(3, 6) and (-3, 4).
AB = AC
AB2 = AC2
⇒ (x – 3)2 + (y – 6)2 = (x + 3)2 + (y – 4)2
![]()
⇒ x2 – 6x + 9 + y2 – 12y + 36
⇒ x2 + 6x + 9 + y2 – 8y + 16
⇒ -6x – 6x – 12y + 8y + 36 – 16 = 0
⇒ -12x – 4y + 20 = 0
⇒ -4(3x + y – 5) = 0
⇒ 3x + y – 5 = 0
(∵ -4 ≠ 0)
![]()
Question 8.
If the vertices of a ∆ABC, are (sin2 θ, cos2 θ), (cos2 θ, sin2 θ) and (0, 0) then find the coordinates of the centroid of the triangle.
Solution.
Here A = (sin2 θ, cos2 θ)
= (x1, y1)
B = (cos2 θ, sin2 θ)
= (x2, y2)
C = (0, 0)
= (x3, y3)
The co-ordinates of the centroid be

Question 9.
Find the ratio in which the point (11, 15) divides the line segment joining the points (15, 5) and (9, 20).
Solution.
A(x1, y1) = (15, 5)
B(x2, y2) = (9, 20)
P(x, y) = (11, 15)
m1 : m2 = ?

⇒ 11(m1 + m2) = 9m1 + 15m2
⇒ 15(m1 + m2) = 20m1 + 5m2
⇒ 2m1 = 4m2
⇒ 5m1 = 10m2
⇒ m1 = 2m2
⇒ m1 = 2m2
⇒ \(\frac{m_{1}}{m_{2}}\) = \(\frac{2}{1}\)
= i.e., m1 = m2 = 2 : 1.
Question 10.
Find the coordinates of the point which divides the line segment joining the points (a, b) and (b, a) internally in the ratio of (a – b) : (a + b).
Solution.
Formula,

Question 11.
The mid-points of the sides of a triangle are (1, 2), (0, -1) and (2, -1). Find the coordinates of the vertices of the triangle.
Solution.
Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of ∆ABC. Let (1, 2), (0, -1) and (2, -1) be the mid-points of AB, BC and CA respectively.
Then

x1 + x2 = 2 …..(i)
x2 + x3 = 0 …..(ii)
x3 + x1 = 4 …..(iii)
y1 + y2 = 4 ……(iv)
y2 + y3 = -2 …..(v)
y3 + y1 = -2 ……(vi)
Adding (i), (ii) and (iii) we get
x1 + x2 + x3 = 3.
∴ x3 = 1, x1 = 3 and x2 = -1.
Adding (iv), (v) and (vi) we get
y1 + y2 + y3 = 0.
∴ y3= – 4, y1 = 2 and y2 = 2.
Hence the vertices of the triangle are A(3, 2), B(-1, 2) and C(1, -4) respectively.
![]()
Question 12.
The three vertices of a parallelogram taken in order are (0, -1), (1, 3) and (2, 2) respectively. Find the coordinates of the forth vertex.
Solution.
Let A(0, -1), B(1, 3), C(2, 2) and D(x, y) be the vertices of a parallelogram. Then the mid-points of the diagonals AC and BD have the same co-ordinates.

Hence, the forth vertex of the parallelogram is (1, -2).
Question 13.
Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2 : 3.
Solution.
Let the coordinates of a point are (x, y).
we have, x1 = -1, y1 = 7;
x2 = 4, y2 = -3
and m1 = 2, m2 = 3
∴ By using section formula,

Hence, coordinates of the point are (1, 3)
Question 14.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution.
Let A(1, 2), B(4, y), C(x, 6) and D(3, 5) are the vertices of a parallelogram.

Since, ABCD is a parallelogram.
∴ AC and BD will bisect each other.
Hence, mid-point of AC and mid-point of BD are same point.

⇒ 1 + x = 7 and 8 = 5 + y
∴ x = 6 and y = 3.
Question 15.
Prove that the three points (1, 2), (3, 3) and (-1, 1) are collinear.
Solution.
Three points are collinear if the area of the triangle formed by them is zero.
Here
x1 = 1, y1 = 2
x2 = 3, Y2 = 3
x3 = -1, y3 = 1
Now, area
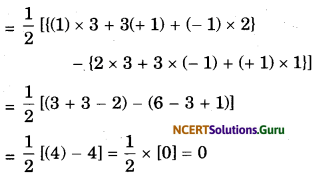
∴ The given three points are collinear.
Question 16.
If the points A(x, y), B(2, 3) and C(3, 4) are collinear, then prove that x + 5y = 17.
Solution.
Here x1 = x, x2 = 2, x3 = -3, y1 = y, y2 = 3, y3 = 4

The points A, B, C are collinear, therefore ∆ = 0.
∴ \(\frac{1}{2}\) (- x – 5y + 17) = 0
⇒ – x – 5y + 17 = 0
⇒ x + 5y = 17.
![]()
Question 17.
For what value of a, the points (1, 4) (a, -2) and (-3, 16) are collinear?
Solution.
The given points are collinear if the area of triangle formed by these three points is zero.
Here, x1 = 1, x2 = a, x3 = -3
y1 = 4, y2 = -2, y3 = 16

Question 18.
Find the area of the triangle whose vertices are
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)
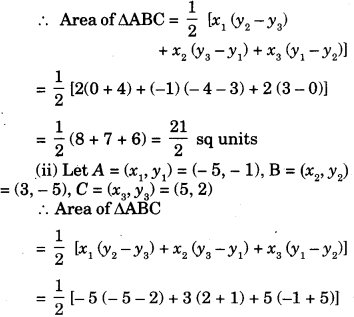

Question 19.
Find the equation of the locus of points equidistant from (-2, 2) and (-4, -2).
Solution.
Let A(-2, 2) and B(-4, -2) be the given points and let P(x, y) be the variable point, Then.
PA = PB PA2 = PB2
⇒ (x + 2)2 + (y – 2)2 = (x + 4)2 + (y + 2)2
⇒ x2 + 2x + 4 + y2 – 2y + 4 = x2 + 8x + 16 + y2 + 4y + 4
⇒ 2x – 2y + 8 = 8x + 4y + 20
⇒ – 6x – 6y – 12 = 0
⇒ x + y + 2 = 0
which is the required equation of the locus.
Question 20.
Find the equation of the locus of all points equidistant from (3, 5) and the x-axis.
Solution.
Let P(x, y) be the variable point, then its distance from x-axis is y and its distance from (3, 5) is
![]()
By the given condition we have
![]()
Squaring on both sides we get
y2 = x2 – 6x + 9 + y2 – 10y + 25
0 = x2 – 6x – 10y + 25
∴ x2 – 6x – 10y + 25 = 0
which is the required equation of the locus.
![]()
Question 21.
Prove that the equation of the locus of a point which moves in such a way that its distance from a point (-g, -f) is always equal to a, is
x2 + y2 + 2gx + 2fy + c = 0,
where x = (g2 + f2 – a2).
Solution.
Let P(x, y) be the variable point on the locus. Then,
![]()
⇒ (x + g)2 + (y + f)2 = a2
⇒ x2 + y2 + 2gx + 2fy + (g2 + f2 – a2) = 0
⇒ x2 + y2 + 2gx + 2fy + c = 0,
where c = (g2 + f2 – a2).
Coordinate Geometry Class 10 Extra Questions Long Answer Type
Question 1.
In a classroom, 4 friends are seated at the points, A, B, C and Das shown in figure. Champ and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square ?” Chameli disagrees. Using distance formula, find which of them is correct.

Solution.
From the given figure, the coordinates of points A, B, C and D are (3, 4), (6, 7), (9, 4) and (6, 1).

Since, the four sides and diagonals are equal. Hence, ABCD is a square.
So, Champa is correct.
![]()
Question 2.
If Q(0, 1) is equidistant from P(5, -3) and R(x, 6), find the values of x. Also, find the distance QR and PR.
Solution.
Since, the point Q (0, 1) is equidistant from P(5, 3) and R(x, 6)
∴ QP = QR
∴ QP2 = QR2
= (5 – 0)2 + (-3 – 1)2 = (x – 0)2 + (6 – 1)2
![]()
⇒ 52 + 42 = x2 + 52
⇒ 25 + 16 = x2 + 25
⇒ x2 = 16
⇒ x = ±4
Thus, R is (4, 6) or (-4, 6).
Now, QR = Distance between Q(0, 1) and R(4, 6)

Question 3.
Find the third vertex of the triangle ABC, if its two vertices are (3,5), (-4, -6) and the coordinates of the centroid are (4, 3).

Solution.
Let the co-ordinates of the third vertex be C(x, y).
Here x1 = 3, x2 = – 4, x3 = x
y1 = 5, y2 = -6, y3 = y

⇒ -1 + x = 12; – 1 + y = 9
⇒ x = 13; y = 10
∴ Co-ordinates of Care (13, 10).
Question 4.
The endpoints of a line segment AB are A(2, 5) and B(1, 9). In what ratio the line segment is drawn through A and B is divided by x-axis and y-axis?
Solution.
For x-axis :
The coordinates of any point on the x-axis are (x, 0).
Let the required ratio be m1 : m2

Hence, the required ratio is 5 : 9. The negative sign represents external division.
For y-axis :
The coordinates of any point on the y-axis are (0, y).
Let the required ratio be m1 : m2

Hence, the required ratio is 2 : 1. The negative sign represents external division.
![]()
Question 5.
A point (2, 3) divides the distance between the points (x, y) and (-5, 4) internally in the ratio 1 : 2. Find the values of x and y.
Solution.

Question 6.
Use analytical geometry to prove that the mid-point of the hypotenuse of a right-angled triangle is equidistant from its vertices.
Solution.
Let AOB be the given right-angled triangle with base OA taken along the x-axis and the perpendicular OB taken along the y-axis.
Let OA = a and OB = b.
Let D be the mid-point of hypotenuse AB.
Then, the coordinates of these points are


⇒ DA = DB = DO.
Question 7.
If the centroid of any triangle ABC be G, then using analytical geometry, prove that AB2 + BC2 + CA2 = 3(GA2 + GB2 + GC2).
Solution.
Let B be the origin, BC be X-axis and through B perpendicular on BC be Y-axis. Then coordinates of B are (0, 0).

Let BC = a, then co-ordinates of Care (a, 0). Let the coordinates of A be (x1, y1), then co-ordinates of the centroid G of ∆ABC are :


![]()
Question 8.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution.
Let A(4, -1) and B(-2, -3) be the line segments and points of trisection of the line segment be P and Question Then,
AP = PQ = BQ = k (Say)
∴ PB = PQ + QB = 2k
and AQ = AP + PQ = 2k

⇒ AP : PB = k : 2k = 1 : 2
and AQ : QB = 2k : k = 2 : 1
Since, P divides AB internally in the ratio 1 : 2. So, the coordinate of P are

and Q divides AB internally in the ratio 2 : 1. So, the coordinates of Q are

So, the two points of trisection are

Question 9.
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along with AD, as shown in figure. Niharika runs \(\frac{1}{4}\)th the distance AD on the 2nd line and posts a green flag. Preet runs \(\frac{1}{5}\)th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

Solution.
From the above figure, the position of green flag posted by Niharika is M

Let P be the position of the blue flag posted by Rashmi in the halfway of line segment MN.

Hence, the blue flag is on the fifth line at a distance of 22.5 m above it.
Question 10.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by ( 1, 6).
Solution.
Let the point A(-1, 6) divide the line joining B(-3, 10) and C(6, -8) in the ratio k : 1. Then, the coordinates of A are

⇒ 6k – 3 = – k – 1 and – 8k + 10 = 6k + 6
⇒ 6k + k = – 1 + 3 and – 8k – 6k = 6 – 10
⇒ 7k = 2 and – 14k = -4 ⇒ k = \(\frac{2}{7}\)
So, the point A divides BC in the ratio 2 : 7.
![]()
Question 11.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and Bis (1, 4).
Solution.
Suppose, AB be a diameter of the circle having its centre at C(2, -3) and coordinates of endpoint B are (1, 4).
Let the coordinates of A be (x, y).

Since, AB is diameter.
∴ C is the mid-point of AB.

⇒ y + 4 = -6
⇒ y = -10
Question 12.
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that
AP = \(\frac{3}{7}\)AB and P lies on the line segment AB.
Solution.
According to the question,

Suppose, P(x, y) be the point which divides the line segment joining the points A (-2, -2) and B (2, -4) in the ratio 3 : 4.


Question 13.
Find the coordinates of the points which divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.
Solution.
Let P, Q and R be the points on line segment AB such that
AP = PQ = QR = RB
Let AP= PQ = QR = RB = k .
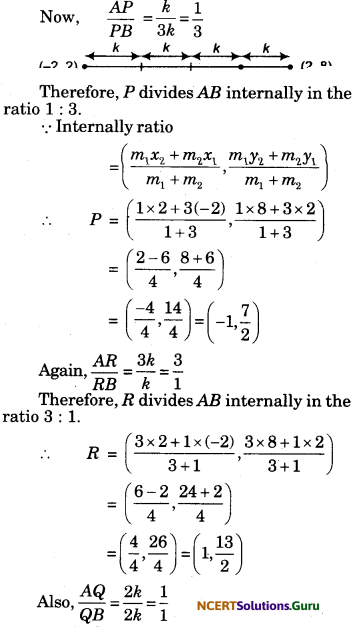
Q is the mid-point of AB.

![]()
Question 14.
The coordinates of three vertices of a ∆ABC are A(3, 4), B(2, -1) and C(4, -6) and the middle points of the three sides BC, CA and AB are respectively, P, Q and R. Prove that:
Area of ∆ABC = 4 (area of ∆PQR).
Solution.
The middle point of BC is


From (i) and (ii), we get
Area of ∆ABC = 4 x area of ∆PQR.
Question 15.
Find the area of a triangle, the coordinates of the mid-points of whose sides are (-2, -1), (1, 6) and (5, 3) respectively.
Solution.
Let ABC be the given triangle and D(-2, -1), E(1, 6) and F(5, 3) be the midpoints of AB, BC and AC respectively.

The co-ordinates of mid-points D, E and F are
Here
x1 = -2, x2 = 1, x3 = 5
y1 = -1, y2 = 6, y3 = 3
Area of ∆DEF

= \(\frac{37}{2}\) square unit.
Area of ∆ABC = 4 × ar (∆DEF)
= 4 × \(\frac{37}{2}\)
= 74 square units.
Question 16.
Median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A (4, -6), B (3, – 2) and C (5, 2).
Solution.
According to the question, AD is the median of ∆ABC, therefore D is the midpoint of BC.


(∵ Area of triangle is positive) .
∵ Area of ∆ADC = Area of ∆ABD
Hence, the median of the triangle divides it into two triangles of equal areas.
Question 17.
Find the locus of the point P(x, y) when :
(i) x = 3
(ii) y = 5
(iii) x = y
Solution.
(i) The given condition is x = 3.
As y is not restricted, it can take any real value between – ∞ to ∞ i.e., – ∞ < y < ∞.

Hence, in the figure the line AB is the required locus.
(ii) The condition given in the question is y = 5. As x is not restricted, it can take any real value between -∞ and ∞ i.e., -∞ < x < ∞.
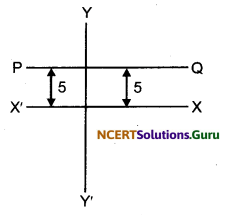
Hence, in the figure the line PQ is the required locus.
(iii) The given condition is x = y. If x takes the values – 2, -1, 0, 1, 2, then y will also take the values -2, -1, 0, 1, 2 respectively. Therefore, the points (-2, -2), (-1, -1), (0, 0), (1, 1) and (2, 2) will satisfy the above condition. Hence, AB will be the required locus.

![]()