Some Applications of Trigonometry Class 10 MCQ Questions with Answers
Question 1.
A pole 6 m high casts a shadow 2√3 m long on the ground, then the Sun’s elevation is :
(A) 60°
(B) 45°
(C) 30°
(D) 90°
Answer:
(A) 60°
Explanation:
In ∆ABC, ∠B = 90°
tanθ = \(\sqrt{3}\) = √3 = tan 60° ⇒ θ = 60°

Question 2.
The angle of depression of a car parked on the road from the top of 150 m high tower is 30°. The distance of the car from the tower (in metres) is :
(A) 50 √3
(B) 150 √3
(C) 150 √2
(D) 75
Answer:
(B) 150 √3
Explanation:
∆ABC, ∠B = 90°
tan 30° = \(\frac{150}{x}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{150}{x}\)
x = 150 √3 m

Question 3.
The length of a string between a kite and a point on the ground is 85 m. If the string makes an angle θ with the ground level such that tan θ = \(\frac{15}{8}\) , then the kite is at what height from the ground ?
(A) 75 m
(B) 79.41 m
(C) 80 m
(D) 72.5 m
Answer:
(A) 75 m
Explanation:
tan θ = \(\frac{15}{8}\)
sin θ = \(\frac{15}{17}\)
Now, sin θ = \(\frac{x}{85}\)
From, equation (i) and (ii),
\(\frac{15}{17}\) = \(\frac{x}{85}\)
x = 75 m

Question 4.
If the height of a vertical pole is √3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is :
(A) 30°
(B) 60°
(C) 45°
(D) 75°
Answer:
(B) 60°
Explanation:
Let the length of shadow is x, Then height of pale = √3 x
tan θ = \(\frac{C B}{A B}\)
tan θ = \(\frac{\sqrt{3} x}{x}\)
tan θ = √3
tan θ = tan 60°
θ = 60°

![]()
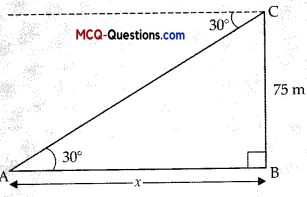
Question 5.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is :
(A) 25 √3
(B) 50 √3
(C) 75 √3
(D) 150
Answer:
(C) 75 √3
Explanation:
In ∆ABC, ∠B = 90°
tan θ = \(\frac{C B}{A B}\)
tan 30° = \(\frac{75}{x}\)
\(\frac{1}{\sqrt{3}}\) = \(\frac{75}{x}\)
x = 75 √3 m
Question 6.
From the top of a cliff 20 m high, the angle of elevation of the top of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is :
(A) 20 m
(B) 40 m
(C) 60 m
(D) 80 m
Answer:
(B) 40 m
Explanation:
In ∆ABC, √A = 90°
tan θ = \(\frac{C A}{A B}\)
tan θ = \(\frac{20}{x}\)
x = \(\frac{20}{\tan \theta}\) ….. (i)

In ∆CDE, √D = 90°
Now, tan 0 = \(\frac{E D}{C D}\)
tan 0 = \(\frac{h-20}{x}\)
x = \(\frac{h-20}{\tan \theta}\) …….(ii)
from equation (i) and (ii),
\(\frac{h-20}{\tan \theta}\) = \(\frac{20}{\tan \theta}\)
h – 20 = 20
h = 40 m
Assertion and Reason Based MCQs
Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.
(A) Both A and R are true and R is the correct explanation of A
(B) Both A and R are true but R is NOT the correct explanation of A
(C) A is true but R is false
(D) A is false and R is True
Question 1.
Assertion (A): If the ratio of the length of a vertical rod and the length of its shadow is 1 : √3, then the angle of elevation of the sun at that moment is 30°.
Reason (R): If the ratio of the height of a tower and the length of its shadow on the ground is √3 : 1, then the angle of elevation of the sun is 60°.
Answer:
(B) Both A and R are true but R is NOT the correct explanation of A
Explanation:
In case of assertion:
Let AB be a vertical rod and BC be its shadow. From the figure, ∠ACB = θ
In ∆ABC,

tan θ = \(\frac{A B}{B C}\)
tan θ = \(\frac{1}{\sqrt{3}}\)
∴ \(\frac{A B}{B C}\)=\(\frac{1}{\sqrt{3}}\)
tan = tan 30°
θ = 30°
∴Assertion is correct.
IN case of reason:

LEt the height of tower be AB and its shadow be BC.
∴\(\frac{B C}{A B}\) = tan θ
= \(\frac{\sqrt{3}}{1}\)
= tan 60°
Hence, the angle of elevation of are correct but reason iss not the correct explanation for assertion.
![]()
Question 2.
Assertion (A): A ladder 15 m long lust reaches the top of a vertical wall. If the ladder makes an angle of 60r with the wall, then the height of the wall is 75 m.
Reason (R): If the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°, then the height of the tower is 10 √3 m.
Answer:
(D) A is false and R is True
Explanation:
In case of assertion:
Let AW be the ladder and WL be the wall.
In ∆AWL, ..
cos 60° = \(\frac{x}{15}\)
⇒ \(\frac{1}{2}\) = \(\frac{x}{15}\)
⇒ x = 7 . 5
Hence, the required height of the wall is 7.5 m.
∴Assertion is incorrect.
In case of reason:
Let AB be the tower.

IN ∆ABC,
tan 30 = \(\frac{A B}{30}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{A B}{30}\)
⇒ AB = 10 √3
Hence, the required height of the tower is 10 √3 m.
∴ Reason is correct.
Hence, assertion is incorrect but reason is correct
Question 3.
Assertion (A): If the length of the ladder placed against a wall is twice the distance between the foot of the ladder and the wall, then the angle made by the ladder with the horizontal is 60°.
Reason (R): If a tower is 20 m high and its shadow on the ground is 20 √3 long, then the sun’s altitude is 60°.
Answer:
(C) A is true but R is false
Explanation:
In case of assertion:
Let the distance between the foot of she ladder Iander and the wall, AB be x.
then AC, the length of the laddre = 2x

IN ∆ABC, ∠B = 90°
cos A = \(\frac{x}{2 x}\)
cos A = \(\frac{1}{2 x}\) = c0s 60°
A = 60°
∴Assertion is incorrect.
In case of reason:
Let the ACB be θ, ∠B = 90°
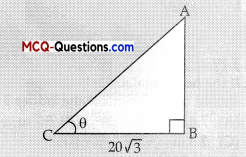
tan θ = \(\frac{A B}{B C}\)
tan θ = \(\frac{20}{20 \sqrt{3}}\) = \(\frac{1}{\sqrt{3}}\) = tan 30°
⇒ θ = 30°
Thus, assertion is correct but reason is incorrect.
Case – Based MCQs
Attempt any four sub-parts from each question. Each sub-part carries 1 mark.
I. Read the following text and Answer: the following question on the basis of the same: An electrician has to repaired an electric fault on the pole of height 5 m. She needs to reach a point 1.3 m below the top of the pole to undertake the repair work (see figure)

Question 1.
What is the length of BD?
(A) 1.3 m
(B) 5 m
(C) 3.7 m
(D) None of these
Answer:
(C) 3.7 m
Explanation:
From figure, the electrician is required to reach at the point B on the pole AD. So, BD – AD – AB
= (5- 1.3) m = 3.7 m
![]()
Question 2.
What should be the length of Ladder, when inclined at an angle of 60° to the horizontal ?
(A) 4.28 m
(B) \(\frac{3.7}{\sqrt{3}}\)
(C) 3.7 m
(D) 7 . 4
Answer:
(A) 4.28 m
Explanation:
In ∆ADC,
sin 60 = \(\frac{B D}{B C}\)
\(\frac{\sqrt{3}}{2}\) = \(\frac{3.7}{B C}\)
BC = \(\frac{3.7 \times 2}{\sqrt{3}}\)
BC = 4 . 28 m(approx)
Question 3.
How far from the foot of pole should she place the foot of the ladder?
(A) 3 . 7
(B) 2 . 12
(C) \(\frac{1}{\sqrt{3}}\)
(D) None of these
Ans.
(B) 2 . 12
Explanation:
In ∆BDC,
cot 60 = \(\frac{D C}{B D}\)
⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{D C}{3.7}\)
⇒ DC = \(\frac{3.7}{\sqrt{3}}\)
⇒ DC = 2 . 14 m (approx)
Question 4.
If the horizontal angle is changed to 30°, then what should be the length of the ladder ?
(A) 7.4 m
(B) 3.7 m
(C) 1.3 m
(D) 5 m
Answer:
(A) 7.4 m
Explanation:
In ∆BDC,
∴ sin 60° = \(\frac{B D}{B C}\)
⇒ \(\frac{1}{2}\) = \(\frac{3.7}{B C}\)
⇒ BC = 3 . 7 x 2 = (90° + 60°)
= 30°
![]()
Question 5.
What is the value of ∠B ?
(A) 60°
(B) 90°
(C) 30°
(D) 180°
Answer:
(C) 30°
Explanation:
In ∆ADC, angle D is 90°. So, by angle sum property.
∠B + ∠D + ∠C = 180° or, ∠B = 180° – (90° + 60°)
= 30°
II. Read the following text and Answer: the following question on the basis of the same:
A group of students of class X visited India Gate on an education trip. The teacher and students had interest in historv as well. The teacher narrated that India Gate, official name Delhi Memorial, originally called All-India War Memorial, monumental sandstone arch in New Delhi, dedicated to the troops of British India who died in wars fought between 1914 and 1919. The teacher also said that India Gate, which is located at the eastern end of the Raj path (formerly called the Kings way), is about 138 feet (42 metres) in height.

Question 1.
What is the angle of elevation if they are standing at a distance of 42 m awav from the monument ?
(A) 30°
(B) 45°
(C) 60°
(D) 0°
Answer:
(B) 45°
Explanation:
Height of INdian gate = 42 m Distance between students and indian gate = 42 cm

Now, tan θ = \(\frac{A B}{B C}\)
tan θ = \(\frac{42}{42}\)
tan θ = 1
tan θ = tan 45°
θ = 45°
Hence, angle of elevation = 45°
![]()
Question 2.
They want to see the tower at an angle of 60°. So, they want to know the distance where they should stand and hence find the distance.
(A) 25.24 m
(B) 20.12 m
(C) 42 m
(D) 24.64 m
Answer:
(A) 25.24 m
Explanation:
Height of India gate = 42 cm ’Angle = 60° Let.the distance between students and India gate = 42 m.

Now, tan 0 = \(\frac{A B}{B C}\)
tan 60 = \(\frac{42}{x}\)
√3 = \(\frac{42}{x}\)
x = \(\frac{42}{\sqrt{3}}\)
x = \(\frac{42 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\)
= \(\frac{42 \sqrt{3}}{3}\)
= 14 3 m = 25. 24 m
Question 3.
If the altitude of the Sun is at 60°, then the height of the vertical tower that will cast a shadow of length 20 m is
(A) 20 √3 m
(B) \(\frac{20}{\sqrt{3}}\)
(C) \(\frac{15}{\sqrt{3}} \mathrm{~m}\)
(D) 15 √3
Answer:
(A) 20 √3 m
Explanation:

Let, the height of tower = h
Now, tan 0 = \(\frac{A B}{B C}\)
tan 60 = \(\frac{h}{20}\)
√3 = \(\frac{h}{20}\)
h = 20 √3
Question 4.
The ratio of the length of a rod and its shadow is 1 : 1. The angle of elevation of the Sun is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Answer:
(B) 45°
![]()
Question 5.
The angle formed bv the line of sight with the horizontal when the object viewed is below the horizontal level is
(A) corresponding angle
(B) angle of elevation
(C) angle of depression
(D) complete angle
Answer:
(A) corresponding angle
III. Read the following text and Answer: the following question on the basis of the same:
A Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka ,them being Nanda Devi(height 7,816 m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite, to the top of Nanda Devi and Mullayanagiri are 30c and 60° respectively. If the distance between the peaks of two mountains is 1937 km, and the satellite is vertically above the midpoint of the distance between the two mountains.

Question 1.
The distance of the satellite from the top of Nanda Devi is
(A) 1118.36 km
(B) 577.52 km
(C) 1937 km
(D) 1025.36 km
Answer:
(A) 1118.36 km
Explanation:

Now, AG = \(\frac{1937}{2}\) km
cos θ = \(\frac{A G}{A F}\)
cos θ = \(\frac{\frac{1937}{2}}{A F}\)
\(\frac{\sqrt{3}}{2}\) = \(\frac{1937}{2 A F}\)
AF = \(\frac{1937}{\sqrt{3}}\)
AF = 1118.36 km
![]()
Question 2.
The distance of the satellite from the top of Mullayanagiri is
(A) 1139.4 km
(B) 577.52 km
(C) 1937 km
(D) 1025.36 km
Answer:
(C) 1937 km
Explanation:
cos θ = \(\frac{P H}{F P}\)
cos 60° = \(\frac{1937}{2 F P}\)
\(\frac{1}{2}\) = \(\frac{1937}{2 F P}\)
FP = 1937 km
Question 3.
The distance of the satellite from the ground is
(A) 1139.4 km
(B) 577.52 km
(C) 1937 km
(D) 1025.36 km
Answer:
(B) 577.52 km
Question 4.
What is the angle of elevation if a man is standing at a distance of 7816 m from Xanda Devi ?
(A) 30°
(B) 45°
(C) 60°
(D) 0°
Answer:
(B) 45°
Explanation:
Height of Nanda Devi Mountain = 7816 m
Distance between man and mountain = 7816 m.

tan θ = \(\frac{A B}{B C}\)
tan θ = \(\frac{7816}{7816}\)
tan θ = 1
tan θ = tan 45°
θ = 45°
![]()
Question 5.
If a mile stone very far away from, makes 45° to the top of Mullanyangiri mountain. So, find the distance of this mile stone from the mountain.
(A) 1118.327 km
(B) 566.976 km
(C) 1937 km
(D) 1025.36 km
Answer:
(C) 1937 km