These NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-8-miscellaneous-exercise/
NCERT Solutions for Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise
![]()
Question 1.
Find the area under the given curves and given lines:
i. y = x², x = 1, x = 2 and x – axis
ii. y = x4, x = 1, x = 5 and x-axis
Solution:

i. The given curves are y = x² , x = 1 and x = 2. The required area lies between the lines x = 1 and x = 2. Hence the limits of integration are 1 and 2.

ii. The given curves are y = x4, x = 1 and x = 5. The required area lies between the lines x = 1 and x = 5. Hence the limits of integration are 1 and 5.

Question 2.
Find the area between the curves y = x and y = x².
Solution:

y = x … (1)
y = x² … (2)
(2) → x = x²
⇒ x² – x = 0 ⇒ x(x – 1) = 0
⇒ x = 0 and x = 1
Hence the limits of integration are 0 and 1. Required area = (Area under the line y = x) – (Area under the parabola y = x²)

![]()
Question 3.
Find the area of the region lying in the first quadrant and bounded by y = 4x², x = 0, y = 1 and y = 4.
Solution:
The given curves are y = 4x²
⇒ x² = \(\frac { y }{ 4 }\) ⇒ x = \(\frac{1}{2} \sqrt{y}\)
x = 0, y= 1, y = 4
The required area lies in the first quadrant between the lines y= 1 and y = 4

Hence the limits of integration are 1 and 4.
Required area = Shaded area

Question 4.
Sketch the graph of y = |x + 3| and evaluate \(\int_{-6}^{0}|x+3| d x\).
Solution:
y = |x + 3| is redefined as follows,

Question 5.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Solution:
The area bounded by the curve y = sinx between x = 0 and x = 2π is shaded in the figure.1

The area bounded by the curve between x = 0 and x = π is same as the area bounded by it between x = π and x = 2π
Required area 2 x Area of the shaded
region above x – axis between x = 0
and π = 2\(2 \int_{0}^{\pi} y d x=2 \int_{0}^{\pi} \sin x d x\)
= 2\([-\cos x]_{0}^{\pi}=-2[\cos x]_{0}^{\pi}\)
= – 2(cos π – cos0) = – 2(- 1 – 1) = 4 sq.unit
![]()
Question 6.
Find the area enclosed between the parabola y² = 4ax and the line y = mx.
Solution:

The curves are y² = 4ax … (1)
and y = mx … (2)
Solving (1) and (2), we get
m²x² = 4ax ⇒ m²x² – 4ax = 0
i.e., x(m²x – 4a) = 0 ⇒ x = 0 or x = \(\frac{4 a}{m^{2}}\)
The x coordinate of the point of intersection
are x = 0 and x = \(\frac{4 a}{m^{2}}\)
Required area = (Area under the parabola y² = 4ax) – (Area under the line y = mx)

Question 7.
Find the area enclosed by the parabola 4y = 3x² and the line 2y = 3x+ 12.
Solution:

The curves are 4y = 3x²
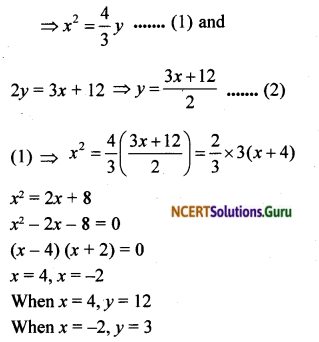
∴ The points of intersection are (4, 12) and (-2, 3)
Required area is shaded in the figure

Question 8.
Find the area of the smaller region bounded by the ellipse \(\frac{x^{2}}{9}+\frac{y^{2}}{4}\) = 1 and the line \(\frac{x}{3}+\frac{y}{2}=1\)
Solution:

\(\frac{x^{2}}{9}+\frac{y^{2}}{4}\) = 1 is the ellipse with centre at origin intersecting the positive x-axis at A(3, 0) and positive y-axis at B(0, 2)

The required area is shaded in the figure.

Question 9.
Find the area of the smaller region bounded by the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) and the line \(\frac{x}{a}+\frac{y}{b}\) = 1.
Solution:

The ellipse intersects the positive x-axis at A (a, 0) and y-axis at B(0, b).

Required area is shaded in the figure.
Required area = Area under the ellipse in the first quadrant – Area under the line AB

![]()
Question 10.
Find the area of the region enclosed by the parabola x² = y, the line y = x + 2 and the x-axis.
Solution:
The given curves are x² = y … (1)
and y = x + 2 … (2)

(1) → x² = x + 2 ⇒ x² – x – 2 = 0
⇒ (x – 2)(x + 1) = 0 ⇒ x = 2, x = – 1
When x = 2, y = 4
When x = – 1, y = 1
The points of intersection are (-1, 1) and (2,4)
Required area is shaded in the figure

Question 11.
Using the method of integration find the area bounded by the curve |x| + |y| = 1.
Solution:

The given curve is |x| + |y| = 1
x + y = 1 … (1)
x – y = 1 … (2)
– x + y = 1 … (3)
– x – y = 1 … (4)
Required area is symmetric w.r.t. both the axes.
Required area = 4 x Area of shaded region
= \(4 \int_{0}^{1}(1-x) d x=4\left[x-\frac{x^{2}}{2}\right]_{0}^{1}\)
= \(4\left(1-\frac{1}{2}\right)=4\left(\frac{1}{2}\right)\)
= 2 sq.units
Question 12.
Find the area bounded by curves {(x, y) : y ≥ x² and y = |x|}
Solution:
The area bounded by the curves y ≥ x² and y = |x| is same as the area bounded by y = x², y = |x| are same

The point B is obtained by solving y = x
and y = x²
i.e., x = x² ⇒ x² – x = 0
x(x – 1) = 0 ⇒ x = 0 or x = 1
When x = 0, y = 0 and when x = 1, y = 1
∴ B is(1, 1)
Required area = 2 x (Area of the shaded portion in the first quadrant)
= 2[(Area under the line y = x) – (Area under the parabola y = x²)]
= \(2\left[\int_{0}^{1} x d x-\int_{0}^{1} x^{2} d x\right]=2\left[\left[\frac{x^{2}}{2}\right]_{0}^{1}-\left[\frac{x^{3}}{3}\right]_{0}^{1}\right]\)
= \(2\left(\frac{1}{2}-\frac{1}{3}\right)=2\left(\frac{1}{6}\right)=\frac{1}{3} \text { sq.unit }\)
![]()
Question 13.
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B(4, 5) and C(6,3).
Solution:

Equation of BC: y – 5 = \(\left(\frac{3-5}{6-4}\right)\)(x – 4)
y – 5 = – (x – 4) ⇒ y = 9 – x
Equation of AC : y – 0 = \(\left(\frac{3-0}{6-2}\right)\)(x – 2)
y = \(\frac{3}{4}\)(x – 2)
Area of ∆ABC = Area under AB + Area under BC – Area under AC

= 5 + 8 – 6 = 7 sq. unit
Question 14.
Using the method of integration find the area of the region bounded by lines:
2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Solution:

The given lines are 2x + y = 4 … (1)
3x – 2y = 6 … (2)
x – 3y + 5 = 0 … (3)
Solving (1) and (2), we get x = 2, y = 0
Let A be the point (2, 0)
Solving (2) and (3), we get x = 4, y = 3
Let B be the point (4, 3)
Solving (1) and (3), we get x = 1, y = 2
Let C be the point (1, 2)
Equation of AB is y = \(\frac{3x-6}{2}\)
Equation of BC is y = \(\frac{x+5}{3}\)
Equation of AC is y = 4 – 2x
Area of ∆ABC Area of trapezium DCBE – Area of ∆DCA – Area of ∆ABE

![]()
Question 15.
Find the area of the region \(\left\{(x, y): y^{2} \leq 4 x, 4 x^{2}+4 y^{2} \leq 9\right\}\)
Solution:

circle with centre at origin and intersecting positive x-axis at C(\(\frac{3}{2}\), 0)
Solving 4x² + 4y² = 9 and y² = 4x, we get 4x² + 16x = 9 ⇒ 4x² + 16x – 9 = 0

Area of the shaded region = Area under OA + Area under AC

The required region is symmetric with respect to jt-axis.
∴ Required area = 2 x shaded area
= \(2\left(\frac{\sqrt{2}}{12}+\frac{9 \pi}{16}-\frac{9}{8} \sin ^{-1}\left(\frac{1}{3}\right)\right)\)
= \(\frac{\sqrt{2}}{6}+\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1}\left(\frac{1}{3}\right) \text { sq.unit }\)
Question 16.
Area bounded by the curve y = x³, the x- axis and the ordinates x = – 2 and x = 1 is
a. – 9
b. \(\frac{-15}{4}\)
c. \(\frac{15}{4}\)
d. \(\frac{17}{4}\)
Solution:
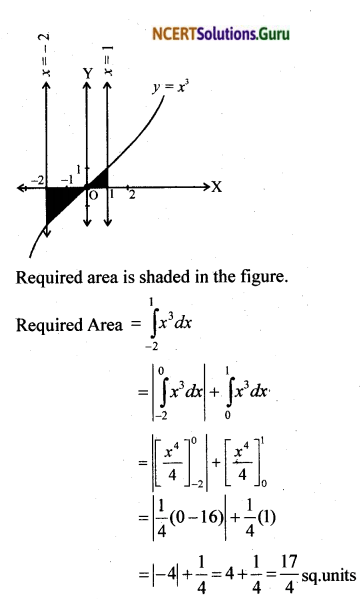
Question 17.
The area bounded by the curve y = x|x|, x-axis and the ordinates x = – 1 and x = 1 is given by
a. 0
b. \(\frac{1}{3}\)
c. \(\frac{2}{3}\)
d. \(\frac{4}{3}\)
Solution:
y = x|x| is redefined as

![]()
Question 18.
The area of the circle x² + y² = 16 exterior to the parabola y² = 6x is
a. \(\frac{4}{3}(4 \pi-\sqrt{3})\)
b. \(\frac{4}{3}(4 \pi+\sqrt{3})\)
c. \(\frac{4}{3}(8 \pi-\sqrt{3})\)
d. \(\frac{4}{3}(8 \pi+\sqrt{3})\)
Solution:
c. \(\frac{4}{3}(8 \pi-\sqrt{3})\)

x² + y² = 16 is a circle with centre at origin
and intersecting positive x-axis at C(4,0).
Solving x² + y² = 16 and y² = 6x, we get
x² + 6x = 16
x² + 6x – 16 = 0 ⇒ (x + 8)(x – 2) = 0
∴ x = – 8 and x = 2
But x = – 8 is not possible ∴ x = 2
When x = 2, y² = 12 ∴ y = ±2\(\sqrt{3}\)
The points of intersection are
A(2, \(\sqrt{3}\)) and B(2, -2\(\sqrt{3}\))
The required area is shaded in the figure.
The nonshaded region OACBO is symmetric w.r.t. x-axis and lies between x = 0 and x = 4.
∴ Area of the nonshaded region = 2 x Area of the nonshaded region in the first quadrant.
= 2 [Area under OA + Area under AC]

Question 19.
The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ \(\frac { π }{ 2 }\) is
a. 2(\(\sqrt{2}\) – 1)
b. \(\sqrt{2}\) – 1
c. \(\sqrt{2}\) + 1
d. \(\sqrt{2}\)
Solution:
b. \(\sqrt{2}\) – 1

The curves are y = sinx … (1)
and y = cos x … (2)
From (1) and (2), we get sin x = cos x
⇒ x = \(\frac { π }{ 4 }\)
∴ y = sin\(\frac { π }{ 4 }\) = \(\frac{1}{\sqrt{2}}\)
Point of intersection of curves is (\(\frac { π }{ 4 }\), \(\frac{1}{\sqrt{2}}\))
Required area = Area of the shaded region = (Area under the curve y = cos x) – (Area above the curve y = sinx)
