These NCERT Solutions for Class 7 Maths Chapter 1 Integers InText Questions and Answers are prepared by our highly skilled subject experts.
NCERT Solutions for Class 7 Maths Chapter 1 Integers InText Questions
NCERT In-text Question Page No. 2
Question 1.
A number line representing integers is given below:

-3 and -2 are marked by E and F respectively. Which integers are marked by B, D, H, J, M and O?
Answer:
Let us complete the given number line such that integers marked by various alphabets are shown

The integer marked by B = -6
The integer marked by D = -4
The integer marked by H = 0
The integer marked by J = 2
The integer marked by M = 5
The integer marked by O = 7
![]()
Question 2.
Arrange 7, -5, 4, 0 and -4 in ascending order and then mark them on a number line to check your answer.
Answer:
(i) Since every positive integer is greater than 0.
(ii) every negative integer is less than 0
-5 < (-4) < 0 < 4 < 7
ascending order is : -5, -4, 0, 4, 7

NCERT In-text Question Page No. 3
Question 1.
We have have done various patterns with numbers in our previous class. Can you find a pattern for each of the following? If yes, complete them.
(a) 7, 3, -1, -5, -9, -13, -17
(b) -2, -4, -6, -8, -10, -12, -14
(c) 15, 10, 5, 0, -5, -10, -15
(d) -11,-8, -5, -2, 1, 4, 7
NCERT In-text Question Page No. 8
Question 1.
Write a pair of integers whose sum gives
(a) a negative integer
(b) zero
(c) an integer smaller than both the integer.
(d) an integer smaller than only one of the integers.
(e) an integer greater than both the integers.
Answer:
(a) -7 and 2
sum = -7 + 2 = -5 (negative integer)
(b) -13 and 13
sum = -13 + 13 = 0
(c) – 13 and (- 7)
sum = – 13 + (-7) = – 13 – 7 = -20
(- 20 is smaller than – 13 and (-7))
(d) 7 and -5
sum = 7 + (-5) = 7 – 5 = 2
(2 is smaller than 7 only)
(e) 19 and 21
sum = 19 + 21 = 40
(40 is greater than both 19 and 21)
![]()
Question 2.
Write a pair of integers whose difference gives
(a) a negative integer.
(b) zero
(c) an integer smaller than both the integers.
(d) an integer greater than only one of the integers.
(e) an integer greater than both the integers.
Answer:
(a) 7 and -12
Difference = – 12 – (7) = -12 -7
= -19 (is a negative integer)
(b) (-3) and (-3)
Difference = -3 – (-3) = – 3 + 3 = 0
(c) 5 and 9 Difference = 9 – 5
= 4 (4 is smaller than 9 as well as 5)
(d) 16 and 5 Difference =16 – 5
= 11 (11 is greater than 5)
(e) 15 and-6
Difference = 15 – (-6) = 15 + 6
= 21 (21 is greater than 15 as well as -6)
NCERT Index Question Page No. 10
Question 1.
Using number line, find:
(i) 4 × (-8)
(ii) 8 (-2)
(iii) 3 × (-7)
(iv) 10 × (-1)
Answer:
(i) 4 × (-8)

From the number line, we have:
(- 8) + (-8) + (-8) + (-8) = -32
∴ 4 × (-8) = -32
(ii) 8 × (-2)
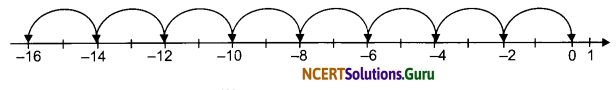
From the number line, we have:
(-2) + (-2) + (-2) + (-2) + (-2) + (-2) + (-2) + (-2) = -16
∴ 8 × (-2) = -16
(iii) 3 × (-7)

From the number line, we have:
(-7) + (-7) + (-7) = -21
3 × (-7) = -21
(iv) 10 × (-1)

From the number line, we have:
(-1) + (-1) + (-1) + (-1) + ( -1) + ( -1) + (-1) + ( -1) + (-1) + (-1) = -10
∴ 10 × (-1) =-10
![]()
NCERT In-text Question Page No. 10
Question 1.
Find:
(i) 6 × (-19)
(ii) 12 × (-32)
(iii) 7 × (-22)
Answer:
(i) 6 × (-19)= – (6 × 19)
= -(114) = -114
(ii) 12 × (-32) = – (12 × 32)
= -(384) = -384
(iii) 7 × (-22) = – (7 × 22)
= -(154) = – 154
NCERT In-text Question Page No. 11
Question 1.
Find:
(a) 15 × (-16)
(b) 21 × (- 32)
(c) (-42) × 12
(d) (-55) × 15
Answer:
(a) 15 × (-16) = -(15 × 16) = -[240] = -240
(b) 21 × (-32) = -(21 × 32) = -[672] = -672
(c) (-42) × 12 = -(42 × 12) = -[504] = -504
(d) (-55) × 15 = -(55 × 15) = -[825] = -825
Question 2.
Check if
(a) 25 × (-21) = (-25) × 21.
(b) (-23) × 20 = 23 × (-20).
Write five more such examples.
Answer:
(a) L.H.S.= 25 × (-21) – (25 × 21)
= – [525] = -525
R.H.S.= (-25) × 21 = – [25 × 21]
= – [525] = -525
∵ L.H.S.= R.H.S.
∴ 25 × (-21)= (-25) × 21
(b) L.H.S.= (-23) × 20 = – [23 × 20]
= – [460] = -460
R.H.S.= 23 × (-20) = – [23 × 20]
= – [460] = – 460
∵ L.H.S.= R.H.S.
∴ (-23) × 20= 23 × (-20)
Other examples:
(i) (-9) × 18 = 9 × (-18)
(ii) 51 × (-40)= (-51) × 40
(iii) (-12) = (-51) × 40
(iv) (-20) × 25= 20 × (-25)
(v) 16 × (-15) = (-16) × 15
![]()
NCERT In-text Question Page No. 12
Question 1.
(i) Starting from (-5) × 4, find (-5) × (-6)
(ii) Starting from (-6) × 3, find (-6) × (-7)
Answer:
(i) Look at the following pattern:
(-5) × 4 = – [5 × 4] = -20
(-5) × 3 = – [5 × 3] = -15 = -20 + 5
(-5) × 2 = – [5 × 2] = -10 = -15 + 5
(-5) × 1 = – [5 × 1] = -5 = -10 + 5
(-5) × 0 = – [5 × 0] = 0 = -5 + 5
From this pattern, we have:
(-5) × (-l) = 0 + 5 = 5
(-5) × (-2) = 5 + 5 = 10
(-5) × (-3) = 10 + 5 = 15
(-5) × (-4) = 15 + 5 = 20
(-5) × (-5) = 20 + 5 = 25
(-5) × (-6) = 25 + 5 = 30
Thus, (-5) × (-6) = 30
(ii) Look at the following pattern:
-6 × 3 = – [6 × 3] = – 18
-6 × 2 = – 12 = – 18 + 6
-6 × 1 = -6 = – 12 + 6
-6 × 0 = 0 = -6 + 6
From this pattern, we have:
-6 × (-1) = 0 + 6 = 5
-6 × (-2) = 6 + 6= 12
-6 × (-3) = 12 + 6= 18
-6 × (-4) = 18 + 6 = 24
-6 × (-5) = 24 + 6 = 30
-6 × (-6) = 30 + 6 = 36
-6 × (-7) = 36 + 6 = 42
Thus, (-6) × (-7) = 42
NCERT In-text Question Page No. 12
Question 1.
(i) Find: (-31) × (-100), (-25) × (-72), (-83) × (-28)
Answer:
We multiply the two negative integers as whole numbers and put the positive sign (+) before the product.
(-31) × (-100) = + [31 × 100] = + [3100] = 3100
(-25) × (-72) = + [25 × 72] = + [1800] = 1800
(-83) × (-28) = + [83 × 28] = + [2324] = 2324
![]()
NCERT In-text Question Page No. 14
Question 1.
(i) The product (-9) × (-5) × (-6) × (-3) is positive whereas the product (-9) × (-5) × 6 × (-3) is negative. Why?
(ii) What will be the sign of the product if we multiply together:
(a) 8 negative integers and 3 positive integers?
(b) 5 negative integers and 4 positive integers?
(c) (-1), twelve timers?
(d) (-1), 2m times, m is a natural number?
Answer:
We know that, if the number of negative integers in a product is even, then the product is a positive integer; if the number of negative integers in a product is odd, then the product is a negative integer.
∴ (i) The product (-9) × (-5) × (-6) × (-3) is positive because an even number of negative integers are multiplied.
The product (-9) × (-5) × 6 × (-3) is negative because an odd number of negative integers are multiplied.
(ii) (a) Positive [ ∵ Product of 8 negative integers is positive]
(b) Negative [ ∵ Product of 5 negative integers is positive]
(c) Positive [ ∵ 12 even and product of even number of negative]
(d) Positive [ ∵ 2m is an even number]
NCERT In-text Question Page No. 18
Question 1.
(i) Is 10 × [(6 + (-2)] = 10 × 6 + 10 × (-2)?
(ii) Is (-15) × [(-7 + (-1)] = (-15) × (-7) + (-15) × (-1)?
Answer:
(i) Yes, [ ∵ a × (b + c) = a × b + a × c]
10 × [6 + (-2) = 10 × [6 – 2]
= 10 × 4 = 40
And, 10 × 6 + 10 × (-2) = 60 – 20 = 40.
Thus, 10 × [6 + (-2) = 10 × 6 + 10 × (-2)
(ii) Yes, [ v a × (b + c) = a × b + a × c]
(-15) × [(-7 + (-1)] = (-15) × [-7 -1]
= (-15) × (-8)
= (+) (15 × 8)
= 120.
And, (-15) × (-7) + (-15) × (-1)
= (+) (15 × 7) + (+) (15 × 1)
= 105 + 15 = 120.
Thus, (-15) × [(-7) + (-1)]
![]()
Question 2.
(i) Is 10 × [6 – (-2)] = 10 × 6 – 10 × (-2)?
(ii) Is (- 15) × [(-7) – (- 1)]
= (-15) × (-7) – (-15) × (-1)?
Answer:
(i) L.H.S = 10 × [6 – (-2)]
= 10 × [6 + 2] = 10 × 8 = 80
R.H.S = 10 × 6 – 10 × (- 2)
= 60 – (-20) = 60 + 20 = 80
∴ L.H.S = R.H.S
(ii) L.H.S = (-15) × [(-7) – (- 1)]
= (-15) × [-7 + 1]
= (-15) × (- 6) = 90
R.H.S = (-15) × (-7) – (-15) × (- 1)
= 105 – (15) = 105 – 15 = 90
∴ L.H.S = R.H.S
NCERT In-text Question Page No. 19
Question 1.
By using distributive property, find: (-49) × 18; (-25) × (-31); 70 × (-19) + (-1) × 70.
Answer:
(i) (-49) × 18
∵ 18 = 10 + 8
∴ (-49) × 18
= (-49) × [10 + 8]
= (-49) × 10 + [-49) × 8
[using distributivity]
= -490 + (-49) [10 – 2] [∵ 8 = 10 – 2]
= -490 + (-49) × 10 – (-49) × 2
= -490 +(-490)+ 98
= -980 + 98 = -882
(ii) (-25) × (-31)
v -31 = (-30) + (-1)
.-. (-25) × (-31)
= (-25) × (-30) + (-1)]
= (- 5) × (-30) + (-25) × (-1)
[using distributivity] = + (25 × 30) + ((25 × 1)]
= 750 + 25 = 775
(iii) 70 × (-19) + (-1) × 70:
Y a × b + a × c = a × [b + c]
70 × (-19) + (-1) × 70
70 × [(-19) + (-1)] = 70 × [-20]
-[70 × 20] = -1400
![]()
NCERT In-text Question Page No. 22
Question 1.
Find:
(a) (-100)+ 5
(b) (-81) + 9
(c) (-75) + 5
(d) (-32) + 2
Answer:
(a) (-100) + 5 = -(100 + 5) = -(20) = -20
(b) (-81) + 9 = -(81 + 9) = -(9) = -9
(c) (-75) + 5 = -(75 + 5) = -(15) = -15
(d) (-32) + 2 = -(32 + 2) = -(16) = -16
NCERT In-text Question Page No. 23
Question 1.
Find:
(a) 125 ÷ (-25)
(b) 80 ÷ (-5)
(c) 64 ÷ + (-16)
Answer:
We know that to divide a positive integer by a negative integer, we first divide them as whole numbers and them put a minus sign (-) before the quotient.
(a) ∵ 125 ÷ 25 = 5
(b) ∵ 80 ÷ 5 = 16
∴ 125 ÷ (-25) = -5
∴ 80 ÷ (-5) = -16
(c) ∵ 64 ÷ 16 = 4
∴ 64 ÷ (-16) = -4
NCERT In-text Question Page No. 23
Question 1.
Find:
(a) (-36) ÷ (-4)
(b) (-201) ÷ (-3)
(c) (-325) ÷ (-13)
Answer:
To divide a negative integer by a negative integer, we first divide them as whole numbers and them put a positive sign (+) before the quotient.
(a) ∵ 36 ÷ 4 = 9
∴ (-36) ÷ (-4) = 9
(b) ∵ 201 ÷ 3 = 67
∴ (-201) ÷ (-3) = 67
(c) ∵ 325 ÷ 13 = 25
∴ (-325) ÷ (-13) = 25
![]()
NCERT In-text Question Page No. 24
Question 1.
Is (i) 1 ÷ a = 1 and (ii) a ÷ (-1) = -a for any integer a? Take different values of a and check.
Answer:
(i) Let us take a = -1, 1, 2, 3,…
For a = -1,
L.H.S. = 1 ÷ (-1) =-l [ ∵ 1 ÷ 1 = 1]
R.H.S. = 1
i. e. L.H.S. ≠ R.H.S.
For a = 2,
L.H.S. = 1 ÷ a = 1 ÷ 2 = \(\frac { 1 }{ 2 }\) ≠ R.H.S.
For a = 3,
L.H.S. = 1 ÷ a = 1 ÷ 3 = \(\frac { 1 }{ 3 }\) ≠ R.H.S.
Thus, 1 ÷ a = 1 is true only for a = 1
(ii) Let us take a = 1,2,3,…
For a = 1,
L.H.S. = a ÷ (-1) = 1 ÷ (-1) = -2
R.H.S. = -a = -1
i.e. L.H.S. = R.H.S.
For a = 2,
L.H.S. = a ÷ (-1) = 2 ÷ (-1) = -2
R.H.S. = a = -2
i.e. L.H.S. = R.H.S.
For a = 7,
L.H.S. = a ÷ (-1) = 3 ÷ (-1) = -3
R.H.S. = -a = -3
i.e. L.H.S. = R.H.S.
For a = 7,
L.H.S. = a ÷ (-1) = 7 + (-1) = -7
R.H.S. = -a = -7
i.e. L.H.S. = R.H.S.
i..e. For every integer, we have a ÷ (-1) = -a