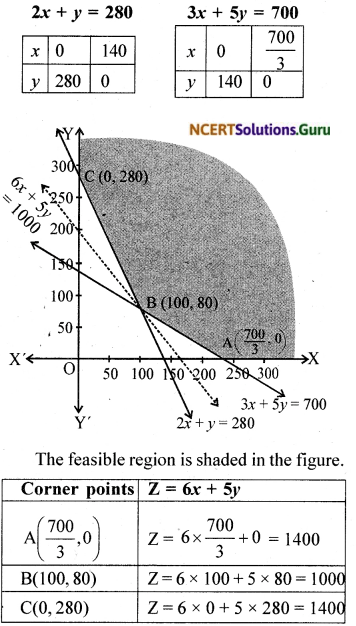
NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming Ex 12.1
These NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming Ex 12.1 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-12-ex-12-1/
NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming Exercise 12.1
![]()
Ex 12.1 Class 12 Question 1.
Maximize Z = 3x + 4y
subject to the constraints:
x + y ≤ 4, x ≥ 0, y ≥ 0.
Solution:
The objective function is Z = 3x + 4y
The constraints are x + y ≤ 4, x ≥ 0, y ≥ 0.
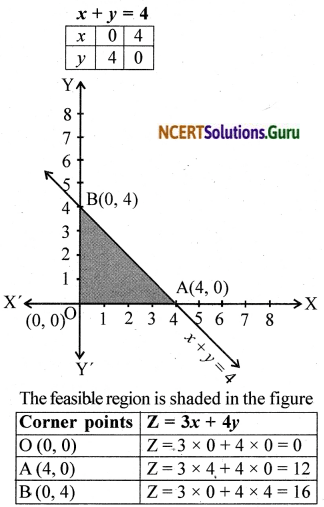
∴ Maximum value of Z is 16 at B (0, 4).
Question 2.
Minimize Z = – 3x + 4y
subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
Solution:
The objective function is Z = – 3x + 4y The constraints are x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
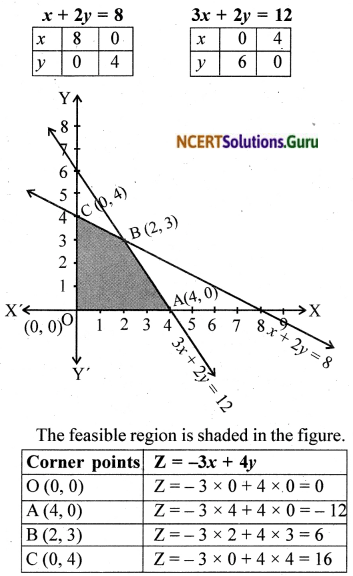
∴ Maximum value of Z is – 12 at A (4, 0).
![]()
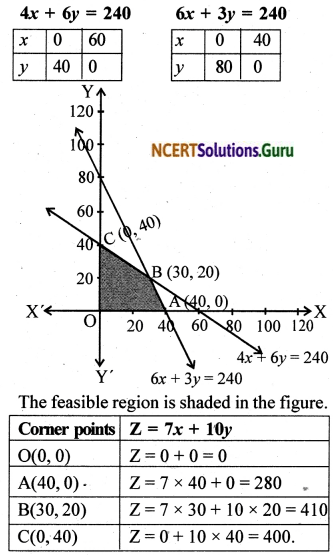
Question 3.
Maximize Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Solution:
The objective function is Z = 5x + 3y
The constraints are 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
The feasible region is shaded in the figure. The point B is obtained by solving the equation 5x + 2y = 10 and 3x + 5y = 15.
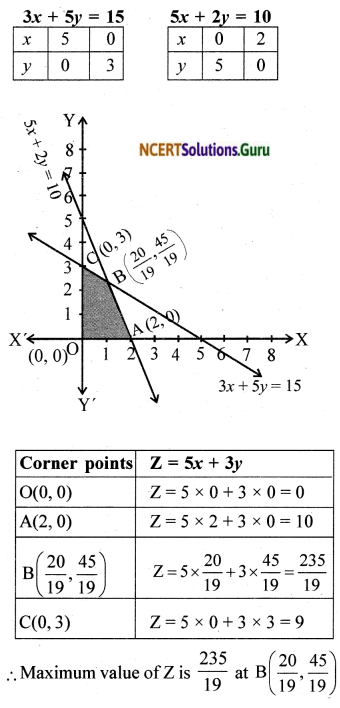
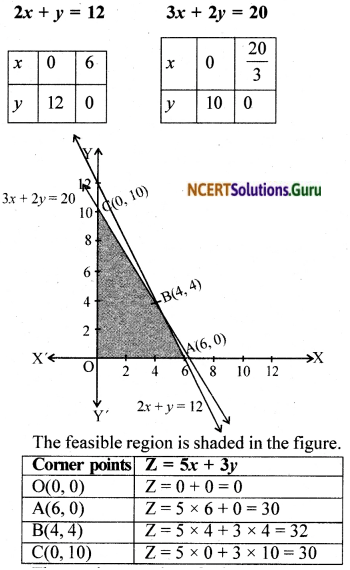
Question 4.
Minimize Z = 3x + 5y such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
Solution:
The objective function is Z = 3x + 5y
The constraints are x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
The feasible region is shaded in the figure.

From the table the minimum value of Z is 7. Since the feasible region is unbounded, 7 may or may not be the minimum value of Z. Consider the graph of the inequality 3x + 5y < 7. This half plane has no point in common with the feasible region. Hence the minimum value of Z is 7 at B (\(\frac { 3 }{ 2 }\), \(\frac { 1 }{ 2 }\))
![]()
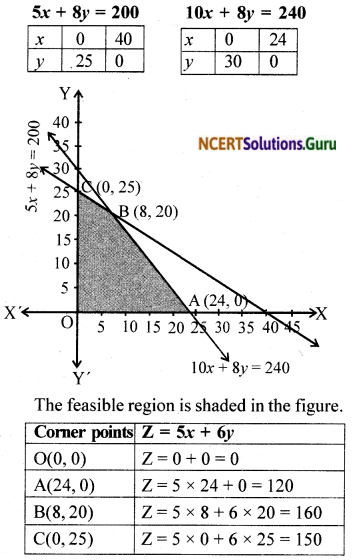
Question 5.
Maximize Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solution:
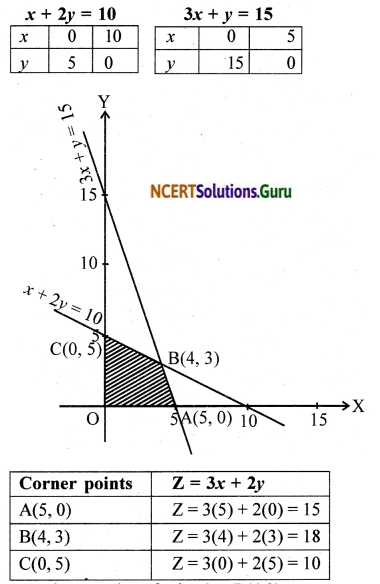
The objective function is Z = 3x + 5y
The constraints are x + 2y < 10,
3x + y ≤ 15, x, y ≥ 0.
The feasible region is shaded in the figure. We use the corner point method to find the maximum of Z
Maximum value of Z is 18 at B(4, 3)
Question 6.
Minimize Z = x + 2y subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Solution:
Consider 2x + y ≥ 3
Let 2x + y = 3
⇒ y = 3 – 2x

(0,0) is not contained in the required half plane as (0, 0) does not satisfy the in equation 2x + y ≥ 3.
Again consider x + 2y ≥ 6
Let x + 2y = 6
⇒ \(\frac { x }{ 6 } +\frac { y }{ 3 }\) = 1
Here also (0,0) does not contain the required half plane. The double-shaded region XABY’ is the solution set. Its comers are A (6,0) and B (0,3). At A, Z = 6 + 0 = 6
At B, Z = 0 + 2 × 3 = 6
We see that at both points the value of Z = 6 which is minimum. In fact at every point on the line AB makes Z = 6 which is also minimum.
![]()
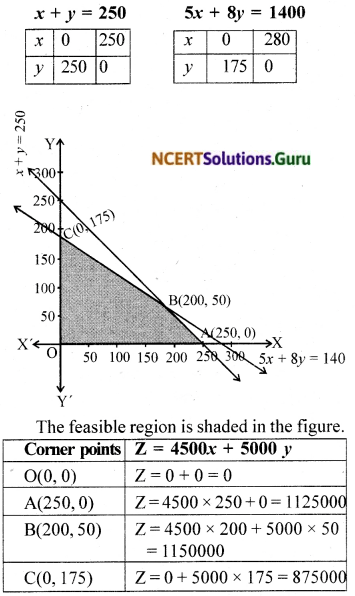
Question 7.
Minimise and Maximise Z = 5x + 10y subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0
Solution:
The objective function is Z = 5x + 10v.
The constraints are x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0
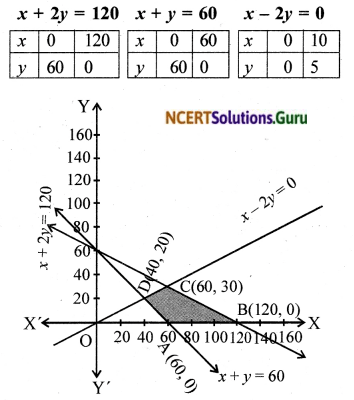
The feasible region is shaded in the figure. We use the comer point method to find the maximum/minimum value of Z.

Minimum value of Z is 300 at A(60,0).
The maximum value of Z is 600 at all points on the line joining B(120, 0) and C(60, 30).
Question 8.
Minimize and maximize Z = x + 2y subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Solution:
The objective function is Z = x + 2y
The constraints are x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0

The feasible region is shaded in the figure. We use corner point method to find maxi-mum/minimum value of Z.

Maximum value of Z is 400 at B(0,200). The minimum value of Z is 100 at all points of the line joining the points (0,50) and (20,40).
Question 9.
Maximize Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0
Solution:

The objective function is Z = – x + 2y
The constraints are x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0
The feasible region is shaded in the figure.

From the table the maximum value of Z is 1. Since the feasible region is unbounded 1 may or may not be the maximum value of Z
Consider the graph of the inequality – x + 2y > 1. This half plane has points common with the feasible region. Hence there is no maximum value for Z.
![]()
Question 10.
Maximize Z = x + y subject to x – y ≤ – 1, – x + y ≤ 0, x, y ≥ 0
Solution:
The objective function is Z = x + y
The constraints are x – y ≤ – 1, – x + y ≤ 0, x, y ≥ 0

There is no point satisfying the constraints simultaneously. Thus the problem has no feasible region. Hence no maximum value for Z.
NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming Ex 12.1 Read More »