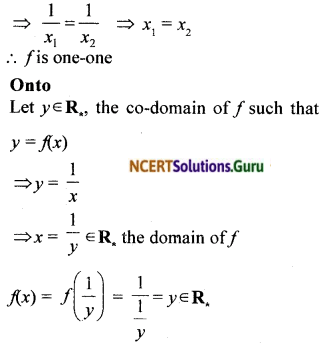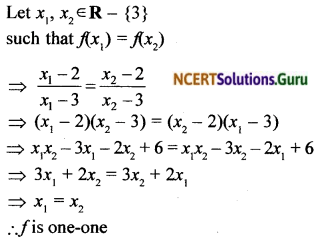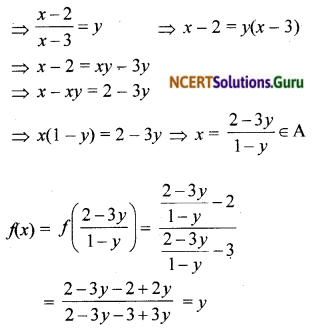CBSE Class 12

These NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.4 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-1-ex-1-4/

NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions 1.4

Ex 1.4 Class 12  Question 1.
Determine whether or not each of the definition of * given below gives a binary operation. In the event that c is not a binary operation, given justification for this.
i. On Z⁺ define * by a * b = a – b
ii. On Z⁺, define * by a * b = ab
iii. On R, define * by a * b = ab²
iv. On Z⁺, define * by a * b = |a – b|
v. On Z⁺, define * by a * b = a
Solution:
i. Let 3, 4 ∈ Z⁺
3 * 4 = 3 – 4 = – 1 ∈ Z⁺
Hence * is not a binary operation.

ii. For every element a, b ∈ Z⁺, ab ∈ Z⁺
Hence * is a binary operation.
Example : 3, 4 ∈ Z⁺, 3 *4 = 3 x 4= 12 ∈ Z⁺

iii. For a, b ∈ R, ab² ∈ R and is unique.
Hence a * b = ab² is a binary operation,
Example : 5, b ∈ R, 5 * 6 = 5 x 6² = 180 ∈ R

iv. For a, b ∈ Z⁺, |a – b| ∈ Z⁺
Hence * is a binary operation.
Example : 3, 4 ∈ Z⁺, 3 * 4 = |3 – 4| = |- 1| = 1 ∈ Z⁺

v. For a, b ∈ Z⁺+, a * b = 2 ∈ Z⁺
Hence * is a binary operation.
Example : 2, 3 ∈ Z⁺, 2 * 3 = 2 ∈ Z⁺

Class 12 Maths Chapter 1 Exercise 1.4 Question 2.
For each binary operation * defined below, determine whether * is commutative or associative.
i. On Z⁺, define a * b = a – b
ii. On Q, define a * b = ab + 1
iii. On Q, define a * b = \(\frac { ab }{ 2 }\)
iv. On Z⁺, define a * b = 2^ab
v. On Z⁺, define a * b = a^b
vi. On R – {- 1}, define a * b = \(\frac { a }{ b+1 }\)
Solution:
i. a * b = a – b; b * a = b – a
∴ a * b * b * a
∴ * is not commutative

Example:
2 * 3 = 2 – 3 = – 1 and 3 * 2 = 3 – 2 = 1
a * (b * c) = a – (b – c) = a – b + c
(a * b) * c = (a – b) – c = a – b – c
∴ a * (b * c) ≠ (a * b) * c
∴ * is not associative

ii. a * b = ab + 1
b * a = ba + 1 = ab + 1 since ab – ba in Q.
∴ a * b = b * a.
Hence * is commutative.
a * (b * c) = a * (bc + 1)
= a(bc + 1) + 1 = abc + a + 1
(a * b) * c = (ab + 1) * c
= (ab + 1)c + 1 = abc + c + 1
∴ a * (b * c) ≠ (a * b) * c
* is not associative.

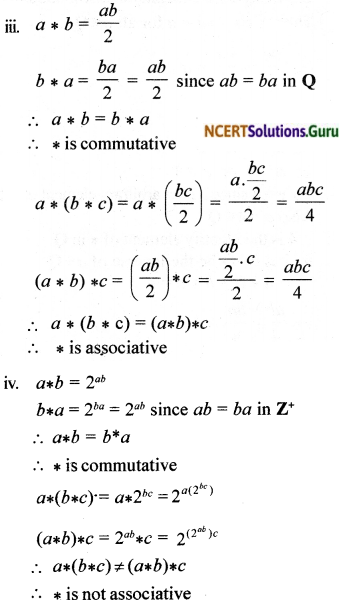
iv. a * b = 2^ab
b * a = 2^ba = 2^ab since ab = ba in Z⁺
∴ a * b = b * a
∴ * is commutative
a * (b * c) = a * 2^bc = 2^a(2bc)
(a * b) * c = 2 ab * c = 2^(2ab)c
∴ a * (b * c) ≠ (a * b) * c.
∴ * is not associative

v. a * b = a^b
b * a = b^b Since a^b ≠ b^a, a * b ≠ b * a
∴ * is not commutative.

Example :
2 * 3 = 2³3 = 8
3 * 2 = 3² = 9
∴ 2 * 3 ≠ 3 * 2
a * (b * c) = a * (b^c) = a(^bc )
(a * b) * c = (ab) * c = (a^b)^c = a^bc
∴ a * (b * c) ≠ (a * b) * c
∴ * is not associative

Hence * is not associative.

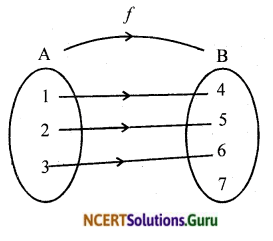
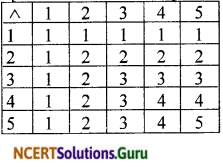
Question 3.
Consider the binary operation ^ on the set {1,2,3,4, 5} defined by a ^ b = min {a, b}. Write the operation table of the operation ^ .
Solution:
1 ^ 1 = min{1, 1} = 1, 1 ^ 2 = min{1, 2} = 1, etc.
2 ^ 1 = min{2, 1} = 1, 2 ^ 2 = min{2, 2} = 2, etc.
3 ^ 1 = min{3,1} = 1, 3 ^ 2 = min{3, 2} = 2, etc. and so on.
The operation table of the operation.

Question 4.
Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table
i. Compute (2 * 3) * 4 and 2 * (3 * 4)
ii. Is * commutative?
iii. Compute (2 * 3) * (4 * 5).

Solution:
i. (2 * 3) * 4 = 1 * 4 = 1
2 * (3 * 4) = 2 * 1 = 1

ii. The entries in the table are symmetric along the main diagonal. Hence * is commutative.

iii. (2 * 3) * (4 * 5) = 1 * 1 = 1

Question 5.
Let *’ be the binary operation on the set {1, 2, 3, 4, 5} defined by a *’ b = H.C.F. of a and b. Is the operation *’ same as the operation * defined in Question 4 above? Justify your answer.
Solution:

*’ gives the same table as given in. Hence * and *’ are the same operations.

Question 6.
Let * be the binary operation on N given by a * b = L.C.M. of a and b. Find
i. 5 * 7, 20 * 16
ii. Is * commutative?
iii. Is * associative?
iv. Find the identity of * in N
v. Which elements of N are invertible for the operation *?
Solution:
i. 5 * 7 = LCM (5, 7) = 5 x 7 = 35
20 * 16 = LCM (20, 16) = 80

ii. a * b = LCM (a, b)
b * a = LCM (b, a) = LCM (a, b)
∴ a * b = b * a
∴ * is commutative

iii. a * (b * c) = a * LCM (b, c)
= LCM (a, b, c)
(a * b) * c = LCM (a, b) * c
= LCM (a, b, c)
∴ a * (b * c) = (a * b) * c
∴ * is associative

iv. Let e be the identity element in N.
Then a * e = e * a = a, for all a ∈ N
⇒ LCM (a, e) = a, for all a ∈ N
⇒ e = 1 ∈ N
∴ 1 is the identity element of * in N.

v. Let a be an invertible element in N.
Then there exists an element b in N such that
a * b = 1 = b * a
⇒ LCM (a, b)= 1
a = b= 1
Thus 1 is an invertible element in N.

Question 7.
Is * defined on the set {1, 2, 3, 4, 5} by a * b = L.C.M. of a and b a binary operation? Justify your answer. (March 2016)
Solution:
a * b = LCM (a, b)
Now 2 * 3 = LCM (2, 3) = 6
But 6 is not an element of the given set.
Hence * is not a binary operation.

Question 8.
Let * be the binary operation on N defined by a * b = H.C.F. of a and b.
Is * commutative? Is * associative?
Does there exist identity for this binary operation on N? (March 2013)
Solution:
a * b = HCF (a, b) for all a, b ∈ N
b * a = HCF (b, a) for all a, b ∈ N
∴ a * b = b * a
∴ * is commutative
a * (b * c) = a * HCF (b, c)
= HCF (a, b, c)
(a * b) * c = HCF (a, b) * c = HCF (a, b, c)
Hence a * (b * c) = (a * b) * c
∴ * is associative
Let e be the identity element in N.
⇒ a * e = e * a = a for all a ∈ N
⇒ HCF (a, e) = HCF (e, a) = a for all a ∈ N
⇒ There is no e e N which makes this true.
⇒ Identity element does not exist in N.

Question 9.
Let * be a binary operation on the set Q of rational numbers as follows:
i. a * b = a – b
ii. a * b = a² + b²
iii. a * b = a + ab
iv. a * b = (a – b)²
v. a * b = \(\frac { ab }{ 4 }\)
vi. a * b = ab²
Find which of the binary operations are commutative and which are associative.
Solution:
i. a * b = a – b b * a = b – a
Hence a * b ≠ b * a
∴ * is not commutative
a * (b * c) = a* (b – c)
= a – (b – c) = a – b + c
(a * b) * c = (a – b) * c = (a – b) – c = a – b – c
Hence (a * b) * c ≠ a * (b * c)
∴ * is not associative.

ii. a * b = a² + b²
b * a = b² + a² = a² + b² = a * b
∴ * is commutative.
a * (b * c) = a * (b² + c²) = a² + (b² + c²)²
(a * b) * c = (a² + b²) * c
= (a² + b²)² + c² ≠ a² + (b² + c²)²
∴ * is not associative

iii. a * b = a + ab;
b * a = b + ba
a * b ≠ b * a
∴ * is not commutative.
a * (b * c) = a * (b + bc)
= a + a(b + bc) = a + ab + abc
(a * b) * c = (a + ab) * c
= (a + ab) + (a + ab)c
= a + ab + ac + abc
a*(b + c) ≠ (a * b) * c
∴ * is not associative.

iv. a * b = (a – b)² = a² – 2ab + b²
b * a = (b – a)² = b² – 2ab + a²
= a² – 2ab + b² = a * b
∴ * is commutative.
a * (b * c) = a * (b – c)² = [a – (b – c)²]²
(a * b) * c = (a – b)² * c = [(a – b)² – c]²
a * (b * c) ≠ (a * b) * c
∴ * is not associative.

v. a * b = \(\frac { ab }{ 4 }\)
b * a = \(\frac { ba }{ 4 }\) = \(\frac { ab }{ 4 }\) = a * b
∴ * is commutative.

vi. a * b = ab² ; b * a = ba²
a * b ± b * a
∴ * is not commutative.
a * (b * c) = a * (bc²) = a(bc²)² = ab²c⁴
(a * b) * c = (ab²) * c = (ab²)(c²) = ab²c²
a * (b * c) ≠ (a * b) * c
∴ * is not associative.

Question 10.
Show that none of the operations given in Question No. 9 (except (v)) has identity.
Solution:
i. Let e be the identity element.
a * e = e * a = a
⇒ a² + e² = e² + a² = a
which is not possible for any e ∈ Q.
∴ There is no identity element.

ii. Let e be the identity element.
a * e = e * a = a
⇒ (a – e)² = (e – a)² = a
which is not possible for any e ∈ Q.
∴ There is no identity element. .

iii. Let e be the identity element.
a * e = e * a = a
⇒ ae² = ea² = a
which is not possible for any e ∈ Q. (SAY 2014)
∴ There is no identity element.

Question 11.
Let A = N x N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d)
Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution:
(a, b) * (c, d) = (a + c, b + d)
(c, d) * (a, b) = (c + a, d+ b) = (a + c, b + d)
(a, b) * (c, d) = (c, d) * (a, b)
∴ * is commutative.
Let (a, b), (c, d), (e, f) ∈ A.
(a, b) * [(c, d) * (e, f)]
= (a, b) * [(c + e, d +f)]
= (a + c + e, b + d +f)
[(a, b) * (c, d)] * (e, f) = (a + c, b + d) * (e, f)
= (a + c + e, b + d + f)
i.e., (a, b) * [(c, d) * (e, f)] = [(a, b) * (c, d)] * (e, f)
∴ * is associative.
Here identity element does not exist.
Let (e₁, e₂) ∈ be the identity element for * in A.
∴ (a, b) * (e₁ + e₂) = (e₁, e₂) * (a, b) = (a, b)
⇒ (a + e₁, b + e₂) = (e₁ + a, e₂ + b) = (a, b)
⇒ a + e₁ = a and b + e₂ = b
⇒ e₁ = 0 and e₂ = 0
(e₁, e₂) = (0, 0) ∉ A, since A = N x N
Hence there is no identity element for * in A.

Question 12.
State whether the following statements are true or false. Justify.
i. For an arbitrary binary operation * on a set N, a * a = a for all a ∈ N
ii. If * is a commutative binary operation on N, then
a * (b * c) = (c * b) * a.
Solution:
i. False
Let a * b = a + b, a, b ∈ N
∴ a * a = a + a = 2a ≠ a

ii. True
Since * is commutative b * c = c * b
∴ a * (b * c) = a * (c * b) = (c * b) * a

Question 13.
Consider a binary operation * on N defined as a * b = a³ + b³. Choose the correct answer.
a. Is * both associative and commutative?
b. Is * commutative but not associative?
c. Is * associative but not commutative?
d. Is * neither commutative nor associative?
Solution:
b. Is * commutative but not associative?
a * b = a³ + b³ = b³ + a³ = b * a
∴ * is commutative.
a * (b * c ) = a * (b³ + c³) = a³ + (b³ + c³)³
(a * b) * c = (a³ + b³) * c = (a³ + b³)³ + c³
* is not associative.

These NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions Miscellaneous Exercise Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-1-miscellaneous-exercise/

NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions Miscellaneous Exercise

Question 1.
Let f : R → R be defined as f(x) = 10x + 7. Find the function g : R → R such that g o f = fog = 1_R.
Solution:
Let y ∈R such that y = 10x + 7
⇒ 10x = y – 7
⇒ x = \(\frac { y -7 }{ 10 }\) ∈ R
Let g(x) = \(\frac { y -7 }{ 10 }\)
(fog)(x) = f(g(x)) = f(\(\frac { y -7 }{ 10 }\))
= 10(\(\frac { y -7 }{ 10 }\) ) + 7 = x
Similarly (gof)(x) = x
Thus (fog) = (gof) = I_R

Question 2.
Let f : W → W be defined as f(n) = n – 1, if n is odd and f(n) = n + 1, if n is even. Show that/is invertible. Find the inverse off. Here, W is the set of all whole numbers.
Solution:
One-one
Let m and n be two distinct elements of W.
Case i :
When m and n are even
∴ f(m) = m + 1 and f(n) = n + 1
Since m ≠ n, then m + 1 ≠ n + 1
⇒ f(m) ≠ f(n)

Case ii :
When m and n are odd
f(m) = m – 1 and f(n) = n – 1
Since m ≠ n, m – 1 ≠ n – 1
⇒ f(m) ≠ f(n)

Case iii :
When m is odd and n is even
f(m) = m – 1 and f(n) = n + 1
Since m ≠ n, m – 1 ≠ n + 1
⇒ f(m) ≠ f(n)

Case iv :
When m is even and n is odd
f(m) = m – 1 and f(n) = n – 1
Since m ≠ n, m – 1 ≠ n – 1
⇒ f(m) ≠ f(n)
i.e., in any case if m ≠ n, then f(m) ≠ f(n)
Hence f is one-one.

Onto
Let y ∈ W, the co-domain of f
If y is odd, then y – 1 is even
f(y – 1) = y – 1 + 1 = y
If y is even, then y + 1 is odd
f(y + 1) = y + 1 – 1 = y
Hence every element in the co-domain has a preimage in the domain.
Hence f is onto.
i.e., f is one-one and onto, hence f is invertible.
We have proved that f(n – 1) = n, if n is odd and f(n + 1) = n, if n is even
∴ f^-1 = \(\left\{\begin{array}{l}
n-1, \text { if } n \text { is odd } \\
n+1, \text { if } n \text { is even }
\end{array}\right.\)
i.e., f^-1(n) = f(n)
Hence inverse of f is f itself.

Question 3.
If f: R → R is defined by f(x) = x² – 3x + 2, find f(f (x)).
Solution:
f(f(x)) = f(x² – 3x + 2)
= (x² – 3x + 2)² – 3(x² – 3x + 2) + 2
= x⁴ + 9x² + 4 – 6x³ – 12x + 4x² – 3x² + 9x – 6 + 2
= x⁴ – 6x³ + 10x² – 3x

Question 4.
Show that the function
f : R → {x ∈ R : – 1 < x < 1} defined by f(x) = \(\frac{x}{1+|x|}\), x ∈ R is one one and onto function.
Solution:
One-one
The domain of f is R
Let x₁ x₂ ∈ R
Case i :
x₁ ≥ 0, x₂ ≥ 0
Then 1 + x₁ ≠ 1 + x₂

Case ii :

since |x₁| = – x₁ and |x₂| = – x₂ as x₁ ≤ 0 and x₂ ≤ 0
⇒ f(x₁) ≠ f(x₂)

Case iii :

Thus in any case, f(x₁) ≠ f(x₂) when x₁ ≠ x₂
Hence f is one-one

Onto :
Let y ∈ R

i.e, when y ≥ 0, there is \(\frac{y}{1-y}\) ∈ R such that \(f\left(\frac{y}{1-y}\right)\)

case iii.
– 1 < y ≤ 0

i.e, when y < 0, there is \(\frac{y}{1+y}\) ∈ R such that \(f\left(\frac{y}{1-y}\right)\) = y

Question 5.
Show that the function f : R → R given by f(x) = x³ is injective.
Solution:
Let f(x₁) = f(x₂) for x₁, x₂ ∈ R
⇒ x³₁ = x³₂ ⇒ x³₁ – x³₂ = 0
⇒ (x₁ – x₂) (x²₁ + x₁x₂ + x²₂) = 0
⇒ x₁ = x₂
∴ f is one-one (injective)

Question 6.
Give examples of two functions f : N → Z and g : Z → Z such that gof is injective but g is not injective.
Solution:
Let f : N → Z defined by f(x) = x and
g : Z → Z defined by g(x) = |x|
We have 1 ≠ – 1, but |1| = |- 1|
∴ g(1) = g(- 1)
Hence g is not injective
gof: N → Z
Let x₁, x₂ ∈ N
such that (gof)(x₁) = (gof)(x₂)
⇒ g(f(x₁)) = g(f(x₂))
⇒ g(x₁) = g(x₂)
⇒ |x₁| = |x₂|
⇒ x₁ = x₂
since x₁, x₂ ∈ N
∴ gof is injective

Question 7.
Give examples of two functions f : N → N and g : N → N such that gof is onto but f is not onto.
Solution:
Let f, g : N → N defined by f(x) = x + 1
g(x) = \(\left\{\begin{array}{l}
x-1 \text { if } x>1 \\
1 \quad \text { if } x=1
\end{array}\right.\)
Let x ∈ N, x ≥ 1 ⇒ x + 1 ≥ 2
⇒ f(x) ≥ 2 for all x ∈ N
Range of f ≠ N
∴f is not onto
gof : N → N
(gof)(x) = g(f(x)) = g(x + 1)
= (x + 1) – 1 since x + 1 > 1 = x
i.e., (gof)x = x for all x ∈ N
i.e., gof is an identity function and hence onto.

Question 8.
Given a non empty set X, consider P(X) which is the set of all subsets of X. Define the relation R in P(X) as follows: For subsets A, B in P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify your answer.
Solution:
ARB if A ⊂ B
i. ARA since A ⊂ A, for all A ∈ P(X) Hence R is reflexive.
ii. ARB need not imply BRA since A ⊂ B
⇒ B ⊄ A . Hence R is not symmetric.
Hence R is not an equivalence relation.

Question 9.
Given a non-empty set X, consider the binary operation * : P(X) x P(X) → P(X) given by A * B = A ∩B for all A, B in P(X), where P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation *.
Solution:
X ∈ P(X)
For any A e P(X), A * X = A ∩ X = A and
X * A= X ∩ A = A
∴ X is the identity element in P(X).
Let S be an invertible element in P(X).
Then S * X = X * S = X
S ∩ X = X ∩ S = X
S = X
∴ X is the only invertible element in P(X).

Question 10.
Find the number of all onto functions from the set {1, 2, 3,…, n} to itself.
Solution:
Since the functions are onto, every element of {1, 2,3 , n} has a pre-image. The element I can have pre-images in n ways. The element 2 can have pre-images in (n – 1) ways and so on. The last element n can have pre-iniage in only one way. Therefore number of ways we can have pre images is n(n – 1)(n – 2) …… 2.1 n! The total number of all onto functions from the set {1, 2, 3, …….. n} to itself is n!.

Question 11.
Let S = {a, b, c} and T = {1, 2, 3}. Find F^-1 of the following functions F from S to T, if it exists.
i. F = {(a, 3), (b, 2), (c, 1)}
ii. F = {(a, 2), (b, 1), (c, 1)}
Solution:
i.

F^-1 : T → S is defined as
F^-1 = {(3, a), (2, b),(1, c)}

ii.

As 1 has 2 preimages, F is not bijective. F^-1 is not defined.

Question 12.
Consider the binary operations *: R x R → R and ° : R x R → R defined as a * b = |a – b| and a ° b = a, for all a, b ∈ R. Show that * is commutative but not associative, ° is associative but not commutative. Further, I show that for all a, b, c ∈ R, a * (b ° c) = (a * b) o (a * b). [If it is so, we say that the j operation * distributes over the operation °]. Does o distribute over *? Justify your answer.
Solution:
Let a, b ∈ R, then
a * b = |a – b| = |b – a| = b * a
i.e., a * b = b * a for all a, b ∈ R
Hence * is commutative.
Let 1, 2, 3 ∈ R
(1 * 2) * 3 = |1 – 2| * 3
= 1 * 3
= |1 – 3| = 2
1 * (2 * 3) = 1 * |2 – 3| = 1 * 1
= |1 – 1| = 0
i.e., (1 * 2) * 3 ≠ 1 * (2 * 3)
∴ * is not associative
Thus * is commutative but not associative.
Let a, b ∈ R
a ° b – a and boa = b
∴ a ° b ≠ b ° a
Hence ° is not commutative.
Now (a ° b) ° c = a ° c = a
a ° (b ° c) = a ° b = a
i.e., a ° (b ° c) = (a ° b) ° c
i.e., o is associative
Hence ° is associative but not commutative.
Let a, b, c ∈ R
a * (b°c) = a * b =|a – b|
(a * b) o (a * c) = |a – b| ° |a – c| = |a – b|
i.e., a * (b°c) = (a * b) ° (a * c)
i.e., * is distributive over °
Now a° (b * c) = a ° |b-c| = a
(a°b) * (a°c) = a * a = |a – a| = 0
i.e., in general a° (b * c) * (a ° b) * (a ° c)
i.e., ° is not distributive over *.

Question 13.
Given a non-empty set X,
let *: P(X) x P(X) → P(X) be defined as A * B = (A – B) ∪ (B – A), for all A, B ∈ P(X). Show that the empty set (Φ) is the identity for the operation * and all the elements A of P(X) are invertible with A^-1 = A.
Solution:

Hence (Φ) is the identity element in P(X)
Now A * A = (A – A) ∪ (A – A)
= Φ∪Φ = Φ
∴ A is the inverse of itself, i.e., A^-1 = A. Hence all the elements of P(X) are invertible with A^-1 = A.

Question 14.
Define a binary operation * on the set {0,1,2,3,4, 5} as a * b = \(\left\{\begin{array}{l}
a+b, \quad \text { if } a+b<6 \\
a+b-6, \text { if } a+b \geq 6
\end{array}\right.\) Show that zero is the identity for this operation and each element a of the set is invertible with 6 – a being the inverse of a.
Solution:
The operation table for * is given below

From the table we observe that a * 0 = 0 * a = a for all a ∈ {0,1,2,3.4,5}. Hence 0 is the identity element for the operation *.
Let a ≠ 0 be any element of {0, 1, 2, 3, 4, 5}.
Then 6 – a ∈ {0, 1, 2, 3, 4, 5}
Now a * (6 – a) = a + 6 – a – 6 = 0
and (6 – a) * a = 6 – a + a – 6 = 0
i.e., a * (6 – a) = (6 – a) * a = 0, identity element of *
∴ 6 – a is the inverse of a ≠ 0.
Hence a ≠ 0 is invertible.
Also the inverse of 0 is 0.

Question 15.
Let A = {- 1, 0, 1, 2}, B = {- 4, – 2, 0, 2} and f, g : A → B be functions defined by f(x) = x² – x, x ∈ A and g(x) = 2|x – \(\frac { 1 }{ 2 }\)| – 1, x ∈ A. Are f and g equal? Justify your answer.
Solution:

Hence fa) = g(a) for all a ∈ A.
∴ f and g are equal functions.

Question 16.
Let A = {1, 2, 3}. Then number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive is
a. 1
b. 2
c. 3
d. 4
Solution:
a. 1
Let R be the relation containing (1, 2) and 0,3)
∴ (1, 2), (1, 3) ∈ R
Since R is reflexive, R contains (1, 1), (2, 2), (3, 3)
Since R is symmetric, R contains (2, 1) and (3, 1)
∴ R = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 1), (3, 1), (3, 3)}
Since R is not transitive (2, 1) and (1, 3) ∈ R but (2, 3) ∉ R.
If (3, 2) ∈ R, then (2, 3) ∈ R since R is symmetric.
∴(3, 2) ∉ R
∴ There is only one relation which is reflexive, symmetric and not transitive.

Question 17.
Let A = {1, 2, 3}. Then number of equivalence relations containing (1,2) is
a. 1
b. 2
c. 3
d. 4
Solution:
b. 2
Given (1, 2) i.e., 1 is related to 2.
Then there are two possibilities.
Case i :
1 is related to 3
A x A= {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3,1), (3, 2), (3, 3)}
Then A x A is reflexive, symmetric and transitive.
∴ A x A is an equivalence relation Containing (1, 2)

Case ii :
1 is not related to 3
Let R= {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3)}
Then R is reflexive, symmetric and transitive, i.e., R is an equivalence relation containing (1 2).
Thus there are two equivalence relations containing (1, 2).

Question 18.
Let f : R → R be the Signum Function defined as
f(x) = \(\left\{\begin{array}{c}
1, x>0 \\
0, x=0 \\
-1, x<0
\end{array}\right.\)
and g : R → R be the Greatest Integer Function given by g (x) = [x], where [x] is greatest integer less than or equal fox. Then, does fog and gof coincide in (0, 1]?
Solution:
(fog)(x) = f(g(x)) = f([x]) x ∈ (0, 1]
= f(0) = 0
(gof)(x) = g(Ax)) = g(1) x ∈ (0,1]
= 1
∴ fog and gof do not coincide in (0, 1]

Question 19.
Number of binary operations on the set {a, b} are
a. 10
b. 16
c. 20
d. 8
Solution:
b. 16
{a, b) x {a, b) contains 4 elements.
Number of relations from {a, b} x {a, b) to {a, b) is 2⁴ = 16

These NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.1 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-1-ex-1-1/

NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions 1.1

Class 12 Maths Chapter 1 Exercise 1.1 Question 1.
Determine whether each of the following relations are reflexive, symmetric and transitive.
i. Relation R in the set A= {1, 2, 3,… 13, 14} defined as R = {(x, y): 3x – y = 0}
ii. Relation R in the set N of natural numbers defined as R = {(x, y): y = x + 5 and x < 4}
iii. Relation R in the set A= (1, 2, 3, 4, 5, 6} as R = {(x, y): y is divisible by x}
iv. Relation R in the set Z of all integers defined as R = {(x, y): x -y is an integer}
v. Relation R in the set A of human beings in a town at a particular time given by
a. R = {(x, y) : x and y work at the same place}
b. R= {(x, y) : x and y live in the same locality}
c. R = {(x, y) : x is exactly 7 cm taller than y}
d. R = {(x, y) : x is wife of y}
e. R = {(x, y) : x is father of y}
Solution:
i. Reflexive R = {(1, 3),(2, 6), (3, 9), (4, 12)}
(1.1) ∈ R
∴ R is not reflexive.

Symmetric
(1, 3) ∈ R but (3, 1) ∉ R
∴ R is not symmetric.

Transitive
(1, 3) ∈ R and (3,9) ∈ R but (1, 9) ∉ R
∴ R is not transitive.
Hence R is neither reflexive, nor symmetric nor transitive.

ii. R = {(1, 6),(2, 7), (3, 8)}
(1, 1) ∉ R
∴ R is not reflexive.
(1, 6) ∈ R but (6, 1) ∉ R
∴ R is not symmetric. In R there does not exist ordered pairs of the form (x, y) and (y, z)
∴ R is transitive.

iii. R = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2.2) , (2,4), (2,6), (3,3), (3,6), (4,4), (5,5), (6,6)}
Reflexive
(x, x) ∈ R for all x ∈ A, since x is divisible by x.
∴ R is reflexive

Symmetric
(1,2) ∈ R but (2, 1) ∈ R
∴R is not symmetric.

Transitive
If y is divisible by x and z is divisible by y, then z is divisible by x. i.e., (x, y) ∈ R
(y, z) ∈R ⇒ (x, z) ∈R for all x, y, z ∈ A
∴R is transitive

iv. Reflexive
x – x = 0, which is an integer
i.e., (x, x)∈ R for every x ∈ Z
∴ R is reflexive

Symmetric
(x, y) ∈ R
⇒ x – y is an integer
⇒ y – x is an integer
⇒ (y, x) ∈ R
∴ R is symmetric
Transitive
(x, y) ∈ R, (y, z) ∈ R ⇒ x – y is an integer and y – z is an integer.
⇒ (x – y) + (y – z) is an integer
⇒ x – z is an integer
⇒ (x, z) ∈ R for all x, y, z ∈ Z
∴ R is transitive.

v. a. Reflexive
(x, x) ∈ R for every x ∈ A, since x and x work at the same place.
∴R is reflexive.

Symmetric
Let (x, y) ∈ R
⇒ x and y work at the same place
⇒ y and x work at the same place
⇒ (y, x) ∈ R for all x, y ∈ A
∴ R is symmetric

Transitive
Let (x, y), (y, z) ∈ R
⇒ x and y work at the same place;
y and z work at the same place.
⇒ x and z work at the same place
⇒ (x, z) ∈ R
∴ R is transitive
Hence R is reflexive, symmetric and transitive.

b. Reflexive, symmetric and transitive
(Similar to v.a)

c. Reflexive
Since x cannot 7 cm taller than x, (x, x) ∉ R.
∴ R is not reflexive

Symmetric
(x, y) ∈ R ⇒ x is exactly 7 cm taller than y
⇒ y cannot be exactly 7 cm taller than x.
⇒ (y, x) ∉ R
∴ R is not symmetric

Transitive
Let (x, y),(y, z) ∈ R ⇒ x is exactly 7 cm
taller than y and y is exactly 7 cm taller than z.
⇒ x is exactly 14 cm taller than z.
⇒ (x, z) ∉ R ∴ R is not transitive.

d. Reflexive
(x, x) ∉ R as x cannot be the wife of x.
∴ R is not reflexive
Symmetric
Let (x, y) ∈ R ⇒ x is the wife of y
⇒ y is not the wife of x ⇒ (y, x) ∉ R
∴ R is not symmetric

Transitive
Let (x, y) ∈ R ⇒ x is the wife of y ⇒ y
cannot be the wife of any z
⇒ (y, z) ∉ R
That is, there does not exist any (x, y) and (y, z) in R.
∴ R is transitive

e. Reflexive
(x, x) ∉ R as x cannot be the father of x.
∴ R is not reflexive

Symmetric
(x, y) ∈ R ⇒ x is the father of y.
⇒ y is not the father of x
⇒ (y, x) ∉ R
∴ R is not symmetric

Transitive
Let (x, y), (y, z) ∈ R ⇒ x is the father of y
and y is the father of z
⇒ x cannot be the father of z
⇒ (x, z) ∉ R
∴ R is not transitive

Chapter 1 Math Class 12 Question 2.
Show that the relation R in the set R of real numbers, defined as R= {(a, b); a<b²} is neither reflexive nor symmetric nor transitive.
Solution:
Reflexive
Let a = \(\frac { 1 }{ 2 }\). Then a² = \(\frac { 1 }{ 4 }\)
⇒ \(\frac { 1 }{ 2 }\) is not less than or equal to (\(\frac { 1 }{ 2 }\))²
⇒ (\(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 2 }\)) ∉ R
∴ R is not reflexive.

Symmetric
Since 1 ≤ 2², (1, 2) ∈ R
But 2 is not less than or equal to 1²
⇒ (2, 1) ∈ R
i.e., (1, 2) ∈ R and (2, 1) ∉ R
∴ R is not symmetric

Transitive
1 ≤ (- 2)² and – 2 ≤ (0)²
But 1 is not less than or equal to 0²
i.e., (1, – 2), (- 2, 0) ∈ R but (1, 0) ∉ R
∴ R is not transitive

Class 12 Maths Ex 1.1 Question 3.
Check whether the relation R defined in the set {1, 2, 3,4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.
Solution:
R={(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}
(1, 1) ∉ R
∴ R is not reflexive
(1, 2) ∈ R and (2, 1) ∉ R
∴ R is not symmetric
(3, 4) ∈ R , (4, 5) ∉ R but (3, 5) ∉ R
∴ R is not transitive

Class 12 Ex 1.1 Question 4.
Show that the relation R in R defined as R = {(a, b); a < b), is reflexive and transitive but not symmetric.
Solution:
Reflexive
(a, a) ∈ R as a < a ∴ R is reflexive
Symmetric
(1, 2) ∈ R ⇒ 1 ≤ 2 ⇒ 2 ≤ 1
⇒ (2, 1) ∉ R
∴ R is not symmetric

Transitive
(a, b), (b, c) ∈ R a ≤ b , b ≤ c
⇒ a ≤ c which is true
∴ R is transitive

Maths Class 12 Chapter 1 Exercise 1.1 Question 5.
Check whether the relation R in R defined by R = {(a,b); a ≤ b³} is reflexive, symmetric or transitive.
Solution:
Reflexive
Let a = \(\frac { 1 }{ 2 }\). Then \(\frac { 1 }{ 2 }\) is not less than (\(\frac { 1 }{ 2 }\))³.
i.e., (\(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 2 }\)) ∉ R
∴ R is not reflexive.

Symmetric
Since 1 ≤ 2³, (1, 2) ∈ R
But 2 is not less than or equal to L³.
⇒ (2, 1) ∉ R
i.e., (1, 2) ∈ R and (2, 1) ∉ R
∴ R is not symmetric

Transitive
9 ≤ 3³ and 3 ≤ 2³, i.e., (9, 3), (3, 2) ∈ R
But 9 is not less than or equal to 2³
i.e., (9, 2) ∉ R
i.e., (9, 3),(3, 2) ∈ R but (9, 2) ∉ R
∴ R is not transitive.

Question 6.
Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Solution:
(1, 1) ∉ R ∴ R is not reflexive
Symmetric
(1, 2), (2, 1) ∈ R ⇒ (2, 1), (1, 2) ∈ R
∴ R is symmetric
Transitive
(1, 2), (2, 1) ∈ R but (1, 1) ∉ R
∴ R is not transitive

Question 7.
Show that the relation R in the set A of all the books in a library of a college, given by ,R = {(x, y) : x and y have same number of pages} is an equivalence relation.
Solution:
Reflexive
(x, x) ∈ R, since book x and x have same number of pages.
∴ R is reflexive

Symmetric
If (x, y) ∈ R, then books x and y have same number of pages i.e., books y and x have same number of pages. Hence (y, x) ∈ R.
∴ R is symmetric

Transitive
Let (x, y, (y, z) ∈ R ⇒ books x, y and books y, z have same number of pages.
⇒ books x and z have same number of pages.
⇒ (x, z) ∈ R
∴ R is symmetric
R is trarisitive R is reflexive, symmetric and transitive. Hence R is an equivalence relation.

Question 8.
Show that the relation R in the set A= {1, 2, 3, 4, 5} given by R = {(a, b) : |a – b| is even}, is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.
Solution:
R= {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (5, 1), (5, 3),(5, 5)}
Reflexive
Since |a – a| = 0 which is even (a, a) ∈ R
∴ R is reflexive

Symmetric
Let (d, b) ∈ R ⇒ |a – b| is even
⇒ |b – a| is even
⇒ (b, a) ∈ R for all a, b ∈ A
∴ R is symmetric

Transitive
Let (a, b), (b, c) ∈ R
⇒ |a – b| is even and |b – c| is even
⇒ |a – c| is even
∴ R is transitive
Hence R is an equivalence relation.
The elements of {1, 3, 5} are related to each other, since |1 – 1|, |1 – 3|, |1 – 5| etc. are even numbers.
The elements of {2, 4} are related to each other, since |2 – 2|, |2 – 4|, |4 – 2|, |4 – 4| are even numbers.
No elements of {1, 3, 5} is related to any element of {2, 4}, since the absolute value of the difference of any element from {1, 3, 5} with any element from {2, 4} is not even.

Question 9.
Show that each of the relation R in the set A= {x ∈ Z : 0 ≤ x ≤ 12}, given by
i. R = {(a, b): |a – b| is a multiple of 4}
ii. R = {(a, b): a = b} is an equivalence relation. Find the set of all elements related to 1 in each case.
Solution:
i. Reflexive
|a – a| = 0 is a multiple of 4, a ∈ A
⇒ (a, a) ∈ R
∴ R is reflexive

Symmetric
Let (a, b) ∈R ⇒ |a – b| is a multiple of 4
⇒ |b – a| is a multiple of 4
⇒ (b, a) ∈R
∴ R is symmetric

Transitive
Let (a, b), (b, c) ∈ R
⇒ |a – b| and |b – c| are multiple of 4
⇒ a- b and b – c are multiple of 4
Now a – c = a – b + b – c
= Multiple of 4 + multiple of 4
= Multiple of 4
∴ |a – c| is a multiple of 4 ⇒ (a, c) ∈R
i.e., (a, b), (b, c) ∈ R ⇒ (a, c) ∈ R
∴R is transitive
Hence R is an equivalence relation.
The set of elements related to 1 is {1, 5,9}

ii. Reflexive
Let a ∈ A. Then a = a
⇒ (a, a) ∈R for all a ∈ A
∴ R is reflexive

Symmetric
Let (a, b) ∈ R ⇒ a – b
⇒ b = a
⇒ (b, a) ∈ R
∴ R is symmetric

Transitive
Let {a, b), (b, c) ∈ R ⇒ a = b and b = c
⇒ a = c
⇒ (a, c) ∈ R
∴ R is transitive.
Hence R is an equivalence relation.
The set of elements related to 1 is {1}

Question 10.
Give an example of a relation, which is
i. Symmetric but neither reflexive nor transitive.
ii. Transitive but neither reflexive nor symmetric.
iii. Reflexive and symmetric but not transitive’
iv. Reflexive and transitive but not symmetric.
v. Symmetric and transitive but not reflexive.
Solution:
Let A= {1, 2, 3}
i. Let R= {(1, 2), (2, 1)}
Reflexive
R is not reflexive, since (1, 1) ∉ R
Symmetric
R is symmetric, since (1, 2), (2, 1) ∈ R
⇒ (2, 1),(1, 2) ∈ R
Transitive
R is not transitive, since (1, 2), (2, 1) ∈R but (1, 1) ∉ R
∴ R is symmetric, but neither reflexive nor transitive.

ii. Let R= {(1,2), (1,3), (3, 2)}
Reflexive
R is not reflexive, since (1, 1) ∉ R
Symmetric
R is not symmetric, since(1, 2) ∈ R, but (2, 1) ∉ R
Transitive
R is transitive, since (1, 3), (3, 2) ∈ R and
(1, 2) ∈ R
∴ R is transitive but neither reflexive nor symmetric.

iii. Let R = {(1, 1), (2, 2), (3, 3), (1, 2),
(2,1) , (2,3), (3,2)}
Reflexive
R is reflexive, since (1,1), (2,2), (3,3) ∈ R
Symmetric
R is symmetric, since (1, 2) ∈ R
⇒ (2, 1) ∈ R(2, 3) ∈ R ⇒ (3, 2) ∈R
Transitive
R is not transitive, since (1, 2), (2, 3) ∈ R but(1, 3) ∉ R
∴ R is reflexive and symmetric but not transitive.

iv. Let R= {(1, 1), (2, 2), (3, 3), (1, 2)}
Reflexive
R is reflexive, since (1, 1), (2, 2), (3, 3) ∈ R
Symmetric
R is not symmetric, since (1, 2) ∈ R but (2, 1) ∉ R
Transitive
R is transitive, since (1, 1), (1, 2) ∈ R and , (1, 2) ∈ R

v. Let R= {(1, 2), (2, 1), (1, 1), (2, 2)}
Reflexive
R is not reflexive, since (3, 3) ∉ R
Symmetric
R is symmetric, since (1, 2) ∈ R ⇒ (2, 1) ∈ R
Transitive
R is transitive, since (1, 2), (2, 1) ∈ R ⇒ (1, 1) ∈ R
and (2, 1 )(1, 2) ∈ R ⇒ (2, 2) ∈ R

Question 11.
Show that the relation R in the set A of points in a plane given by R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.
Solution:
Let O be the origin
Then R = {(P, Q) : OP = OQ}
Reflexive
Let P be a point in the plane Then OP = OP
⇒ (P, P) ∈ R for all P
∴ R is reflexive

Symmetric
Let (P, Q) ∈ R
⇒ OP = OQ
⇒ OQ = OP
⇒ (Q, P) ∈ R
∴ R is symmetric.

Transitive
Let (P, Q), (Q, S) ∈ R
⇒ OP = OQ and OQ = OS
⇒ OP = OS
⇒ (P, S) ∈ R
∴ R is transitive
Hence R is an equivalence relation.
Let P ≠ (0,0) be a point in the plane. Consider the circle with centre at origin and radius OP. Then the set of points on this circle are related to P since the distance from the origin to any point on the circle is OP.
Hence the set of points related to P is the circle passing through P with origin as centre.

Question 12.
Show that the relation R defined in the set A of all triangles as R = {(T₁, T₂) : T₁ is similar to T₂}, is an equivalence relation. Consider three right angled triangles T₁ with sides 3,4, 5, T₂ with sides 5, 12, 13 and T₃ with sides 6, 8,10. Which triangles among T₁, T₁ and T₃ are related?
Solution:
R = {(T₁, T₂): T₁ is similar to T₂
Reflexive
Let T ∈ A
Since T is similar to T, (T, T) ∈ R
∴ R is reflexive

Symmetric
Let (T₁,T₂) ∈ R
⇒ T₁ is similar to T₂
⇒ T₂ is similar to T₁
⇒ (T₂,T₁) ∈ R
∴ R is symmetric

Transitive
Let (T₁, T₂), (T₂, T₃) ∈ R
⇒ T₁ is similar to T₂ and T₂ is similar to T₃
⇒ T₁ is similar to T₃
⇒ (T₁, T₃) ∈ R
∴ R is transitive
Hence R is an equivalence relation.
Two triangles are similar if their sides are proportional. The sides 3, 4, 5 of triangle T₁ is proportional to the sides 6, 8, 10 of triangle T₃
(\(\frac { 3 }{ 6 }\) = \(\frac { 4 }{ 8 }\) = \(\frac { 5 }{ 10 }\))
i. e., the sides of and T₁ are proportional. Hence T₁ is related to T₃.

Question 13.
Show that the relation R defined in the set A of all polygons as R = {(P₁, P₂): P₁ and P₂ have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?
Solution:.
R = {(P₁, P₂): P₁ and P₂ have same number of sides}
Reflexive
Let P ∈ A
Since P and P have same number of sides,
(P, P) ∈ R for all P.
∴ R is reflexive

Symmetric
Let (P₁, P₂) ∈ R
⇒ Number of sides of P₁ = Number of sides of P₂
⇒ Number of sides of P₁ = Number of sides of P₁
⇒ (P₂, P₁) ∈ R
∴ R is symmetric

Transitive
Let (P₁, P₂), (P₂, P₃) ∈ R
⇒ P₁, P₂ have same number of sides and P₂, P₃ have same number of sides.
⇒ P₁, P₃ have same number of sides
⇒ (P₁, P₃) ∈ R
∴ R is transitive
Hence R is an equivalence relation.
The right triangle with sides 3, 4, 5 is a polygon having 3 sides.
∴ T he set of elements of A related to T is the set of triangles in the plane.

Question 14.
Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L₁, L₂) : L₁ is parallel to L₂}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.
Solution:.
Reflexive
(L₁, L₁) ∈R since the line L₁ is parallel to itself.
∴ R is reflexive

Symmetric
(L₁, L₂) ∈ R ⇒ L₁ is parallel to L₂
⇒ L₂ is parallel to L₁ ⇒ (L₂, L₁) ∈ R
∴ R is symmetric.

Transitive
(L₁, L₂) ∈R, (L₂, L₃) ∈ R
L₁, L₂ are parallel and L₂, L₃ are parallel
⇒ L₁ and L₃ are parallel. ⇒ (L₁, L₃) ∈ R
∴ R is transitive.
Hence R is an equivalence relation.
The set of all lines related to the line y = 2x + 4 is the line y = 2x + c where C ∈ R.

Question 15.
Let R be the relation in the set (1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3) , (3, 3), (3, 2)}. Choose the correct answer.
a. R is reflexive and symmetric but not transitive.
b. R is reflexive and transitive but not symmetric.
c. R is symmetric and transitive but not reflexive.
d. R is an equivalence relation.
Solution:
Answer:
b. R is reflexive and transitive but not symmetric.
(1, 2) ∈ R but (2, 1) ∉ R
∴ R is not symmetric

Question 16.
Let R be the relation in the set N given by R = {{a, b) : a = b – 2, b > 6}. Choose the correct answer.
a. (2, 4) ∈ R
b. (3, 8) ∈ R
c. (6, 8) ∈ R
d. (8, 7) ∈ R
Solution:
Ans. c
If b = 8, a = 6 – 2 = 8 – 2 = 6
∴ (6, 8) ∈ R is correct.

These NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.2 Questions and Answers are prepared by our highly skilled subject experts. https://mcq-questions.com/ncert-solutions-for-class-12-maths-chapter-1-ex-1-2/

NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions 1.2

Ex 1.2 Class 12 NCERT Solutions Question 1.
Show that the function f : R_* → R_*, defined by f(x) = \(\frac { 1 }{ x }\) is one-one and onto, where R_* is the set of all non-zero real numbers. Is the result true, if the domain R_* is replaced by N with co-domain being same as R_*?
Solution:
a. One-one
Let x₁, x₁ ∈ R, such that f(x₁) = f(x₂)

For each y ∈ R_* there exists x = \(\frac { 1 }{ y }\) ∈ R,
such that f(x) = y.
∴ f is onto

b. One-one
Let x₁, x₂ ∈ N such that f(x₁) = f(x₂)
⇒ \(\frac{1}{x_{1}}=\frac{1}{x_{2}}\) ⇒ x₁ = x₂
∴ f is one-one
Onto
The domain of f is N = {1, 2, 3, ……. }
The range of f = {1, \(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 3 }\), \(\frac { 1 }{ 4 }\), ……. } ≠ R
∴ f is not onto
Another method
2 ∈ R_*.
The pre-image of 2 is \(\frac { 1 }{ 2 }\) ∉ N .
Hence f is not onto.

Exercise 1.2 Class 12 NCERT Solutions Question 2.
Check the injectivity and surjectivity of the following functions
i. f : N → N given by f (x) = x²
ii. f : Z → Z given by f (x) = x²
iii. f : R → R given by f (x) = x²
iv. f : N → N given by f (x) = x³
v. f : Z → Z given by f (x) = x³
Solution:
i. Injectivity
Let x₁, x₁ ∈ N such that f(x₁) = f(x₂)
⇒ x²₁ = x²₂
⇒ x²₁ – x²₂ = 0
⇒ (x₁ – x₂)(x₁ + x₂) = 0
⇒ x₁ – x₂ = 0 since x₁ + x₂ ≠ 0 as x₁, x₁ ∈ N
⇒ x₁ = x₂
∴ f is injective
Surjectivity
Let y = 3 ∈ N, the co-domain of f
f(x) = 3 ⇒ x² = 3
⇒ x = ±\(\sqrt{3}\) ∉ N , the domain of f
∴f is not surjective

ii. Injectivity
Let x₁ = 2, x₂ = – 2
f(x₁) = 2² = 4, f(x₂) = (- 2)² = 4
i.e., f(x₁) = f(x₂) for x₁ ≠ x₂
∴ f is not injective

Surjectivity
Let y = 2 ∈ Z, the co-domain of f
∴ f(x) = 2 ⇒ x² = 2 ⇒ x = ± \(\sqrt{2}\) ∉ Z, the domain of f
∴ f is not surjective.

iii. Injectivity
Let x₁ = 2, x₂ = – 2
f(x₁) = 2² = 4, f(x₂) = (- 2)² = 4
i.e., f(x₁) = f(x₂) for x₁ ≠ x₂
∴ f is not injective (one-one)

Surjectivity
Let y = – 1 ∈ R, the co-domain of f
f(x) = – 1 ⇒ x² = -1
⇒ x = ± \(\sqrt{1}\) ∉ R, the domain of f
∴ f is not surjective (onto)

iv. Injectivity
Let x₁, x₂ ∈ N such that f(x₁) = f(x₁) = f(x₂)
⇒ x³₁ = x³₂ ⇒ x³₁ – x³₂ = 0
⇒ (x₁ – x₂) (x²₁ + x₁x₂ + x²₂2) = 0
⇒ x₁ – x₂ = 0 since x²₁ + x₁x₂ + x²₂ ≠ 0
⇒ x₁ = x₂
∴f is injective (one-one)

Surjectivity
Let y = 4 ∈ N, the co-domain of f
⇒ f(x) = 4 ⇒ x₃ = 4
⇒ x = 4^1/3 ∉ N, the domain of f
∴f is not surjective (onto)

v. Injectivity
Let x₁, x₂ ∈ Z such that f(x₁) = f(x₂)
⇒ x³₁ = x³₂ ⇒ x₁ = x₂
∴ f is injective (one-one)

Surjectivity
Let y = 4 ∈ Z, the co-domain of f such that
f(x) = 4
⇒ x₃ = 4 ⇒ x = 4^1/3 ∉ Z, the domain of f
∴ f is not surjective (onto)

Exercise 1.2 Class 12 Maths NCERT Solutions Question 3.
Prove that the Greatest Integer Function f : R → R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Solution:
Refer Example 26
One-one
Let x₁ = 2.1, x₂ = 2.5
f(x₁) = f(2.1) = [2.1] = 2
f(x₂) = f(2.5) = [2.5] = 2
i.e. f(x₁) = f(x₂) for x₁ ≠ x₂
∴ f is not one-one.

Onto
Let y = 2.5 ∈ R, the co-domain of f
f(x) = 2.5 ⇒ [x] = 2.5, which is not possible.
∴ f is not onto

Class 12 Maths Ncert Solutions Chapter 1 Ex 1.2 Question 4.
Show that the Modulus Function f : R → R, given by f(x) = |x|, is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is – x, if x is negative.
Solution:
One-one
Let x₁ = 1 and x₂ = – 1 ∈ R
f(x₁) = f(1) = |1| = 1
f(x₂) = f(- 1) = |- 1|= 1
i.e., f(x₁) = f(x₂) for x₁ ≠ x₂
∴ f is not one-one Onto
Let y = – 1 ∈ R, the co-domain of f
f(x) = – 1 ⇒ |x|= – 1 which is not possible
∴ f is not onto.

Class 12 Maths 1.2 NCERT Solutions  Question 5.
Show that the Signum Function f : R → R, given by
\(f(x)=\left\{\begin{array}{c}
1, \text { if } x>0 \\
0, \text { if } x=0 \\
-1, \text { if } x<0
\end{array}\right.\)
is neither one-one nor onto.
Solution:
One-one
Let x₁ = 1, x₂ = 2
f(x₁) = f(1) = 1
f(x₂) = f(2) = 1
i.e. f(x₁) = f(x₂) for x₁ ≠ x₂
∴ f is not one-one

Onto
The co-domain of f is R
The range of f is {-1, 0, 1} ≠ R
∴ f is not onto.

Relation And Function Class 12 Exercise 1.2 Question 6.
Let A = {1, 2, 3}, B = (4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Solution:

Different elements in A have different images in B. Hence f is one – one.

Ex 1.2 Class 12 Maths NCERT Solutions Question 7.
In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
i. f : R → R defined by f(x) = 3 – 4x
ii. f : R → R defined by f(x) = 1 + x²
Solution:
i. One-one
Let x₁, x₂ 6 R such that f(x₁) = f(x₂)
⇒ 3 – 4x₁ = 3 – 4x₂
⇒ – 4x₁ = – 4x₂
⇒ x₁ = x₂
∴f is one-one
Onto
Let y ∈ R, such that y = f(x)
⇒ y = 3 – 4x
⇒ 4x = 3 – y
⇒ x = \(\frac { 3-y }{ 4 }\) ∈ R
f(x) = f\(\frac { 3-y }{ 4 }\) = 3 – 4(\(\frac { 3-y }{ 4 }\))
= 3 – 3 + y = y
For each y ∈ R there exists x = \(\frac { 3-y }{ 4 }\) ∈ R
such that f(x) = y
∴f is onto
Since f is one-one and onto, f is bijective.
Another Method
f(x) = 3 – 4x is a linear function from R to R.
∴ f is one-one and onto.
Hence f is bijective.

ii. One-one
Let x₁ = 1, x₂ = – 1 ∈ R
f(x₁) = f(1) = 1 + 1² = 2
f(x₂)= f(-1) = 1 + (- 1)² = 2
i.e., f(x₁) = f(x₂) for x₁ ≠ x₂
∴f is not one-one

Onto
Let y = – 1 ∈ R, the co-domain of f
f(x) = y ⇒ 1 + x² = – 1
⇒ x² = – 2
⇒ x = ± \(\sqrt{-2}\) ∉ R
∴f is not onto.
Thus f is neither one-one nor onto.

Class 12 Ex 1.2 NCERT Solutions Question 8.
Let A and B be sets. Show that f : A x B → B x A such that f(a, b) = (b, a) is bijective function.
Solution:
Let (a₁, b₁) and (a₂, b₂) ∈ A x B
such that f(a₁, b₁) = f(a₂, b₂)
⇒ (b₁, a₁) = (b₂, a₂)
⇒ b₁ = b₂ and a₁ = a₂
⇒ (a₁, b₁) = (a₂, b₂)
∴f is one-one.
Let (b, a) ∈ B x A ⇒ b ∈ B and a ∈ A
⇒ (a, b) ∈ A x B
f(a, b) = (b, a)
i.e., corresponding to each (b, a) ∈ B x A, there exists (a, b) ∈ A x B such that f(a, b) = (b, a)
∴ f is onto
Hence f is a bijection.

Maths Class 12 Exercise 1.2 NCERT Solutions Question 9.
Let f : N → N be defined by
f(n) = \(\left\{\begin{array}{l}
\frac{n+1}{2}, \text { if } n \text { is odd } \\
\frac{n}{2}, \text { if } n \text { is even }
\end{array} \text { for all } n \in \mathbf{N}\right.\)
State whether the function / is bijective. Justify your answer.
Solution:
Let x₁ = 1 and x₂ = 2 ∈ N
f(x₁) = f(1) = \(\frac { 1+1 }{ 2 }\) = 1 and f(x₂) = f(2) = \(\frac { 2 }{ 2 }\) = 1
∴ f(x₁) = f(x₂) for x₁ ≠ x₂
Hence f is not one-one and hence not bijective.

Class 12 Math Ex 1.2 NCERT Solutions Question 10.
Let A = R – {3} and B = R – {1}. Consider the function f : A → B defined by f(x) = \(\left(\frac{x-2}{x-3}\right)\). Is f one-one and onto? Justify your answer.
Solution:
One-one

One-one
Let y ∈ B such that f(x) = y

For each y ∈ B, there exists x = \(\left(\frac{2-2y}{1-y}\right)\) ∈ A
such that f(x) = y
∴ f is onto.

Relations And Functions Class 12 Exercise 1.2 Question 11.
Let f : R → R be defined as f(x) = x⁴. Choose the correct answer.
a. f is one-one onto
b. f is many-one onto
c. f is one-one but not onto
d. f is neither one-one nor onto.
Solution:
d. f is neither one-one nor onto.

One-one
Let x₁ = 1, x₂ = – 1 ∈ R
f(x₁) = f(1) = (1)⁴ = 1
f(x₂) = f(-1) = (-1)⁴= 1
f(x₁) = f(x₂) for x₁ ≠ x₂
∴ f is not one-one

Onto
The co-domain of f is R.
The range of f is [0, ∞), the non-negative real numbers.
Since range of f ≠ co-domain of f is not onto.
Hence f is neither one-one nor onto.

1.2 Class 12 NCERT Solutions Question 12.
Let f : R → R be defined as f (x) = 3x. Choose the correct answer.
a. f is one-one onto
b. f is many-one onto
c. f is one-one but not onto
d. f is neither one-one nor onto.
Solution:
a. f is one-one onto
f(x₁) = f(x₂) ⇒ 3x₁ = 3x₂ ⇒ x₁ = x₂
∴ f is one-one
For y ∈ co-domain off there exists \(\frac { y }{ 3 }\) in the domain of f such that f(\(\frac { y }{ 3 }\)) – 3(\(\frac { y }{ 3 }\)) = y
Hence f is onto.

Detailed, Step-by-Step NCERT Solutions for Class 12 Sociology Chapter 1 Introducing Indian Society Questions and Answers were solved by Expert Teachers as per NCERT (CBSE) Book guidelines covering each topic in chapter to ensure complete preparation. https://mcq-questions.com/ncert-solutions-for-class-12-sociology-chapter-1/

Introducing Indian Society NCERT Solutions for Class 12 Sociology Chapter 1

Introducing Indian Society Questions and Answers Class 12 Sociology Chapter 1

Question 1.
What are the main problems of national integration in India?
Answer:
The problems of India are linguistic identity, regionalism, demand for separate states and terrorism etc. create hindrances in the way of national integration. Due to these . problems, usually strikes, riots and mutual fights take place, which have posed a severe threat to national unity and integration.

Question 2.
Why is sociology a distinct subject in comparison with all other subjects?
Answer:
Sociology is a subject with which everyone knows something about society. Other subjects are learnt at home, school or elsewhere through instructions but much of our with growth in years as it appears to be acquired naturally or automatically.

Question 3.
What are the basic functions of a society?
Answer:
Sociologists and social anthropologists have adopted the term function from biological sciences where it has been used for certain organic processes necessary for the maintenance of the organisms. Basic functions necessary for continuity and survival of any society are :

• Recruitment of members
• Socialization
• Production and distribution of goods and services and preservation of order.

Question 4.
What do you understand by social structure?
Answer:
A society consists of

• Males and females, adults and children, various occupational and religious groups and so on.
• The interrelationship between various that of parents and children and between various groups.
• Finally, all the parts of the society are put together and system are interrelated and complementary concepts.

Question 5.
Why is the social map provided to us in childhood by the deluding socialization essential?
Answer:
Social maps are provided by our parent siblings, relatives and neighbour. It may be specific and partial. It provides us only with common sense or unlearnt or perceivable knowledge which may or may not be real. A proper use and application of reflexivity is essential for drawing other kinds of maps. It is sociological perspective that teaches us the procedure of drawing social maps, wholesome and exclusive.

Question 6.
What is community identity? Discuss its characteristics.
Answer:
Community that provides us the language and cultural values through which we comprehend the world. It is based on birth and belongings and never on some form of acquired qualification or accomplishment. Birth based identity is called ascriptive because this does not involve any choice on the part of the individual’s concerned.

It is actually worthless and discriminating. These ascriptive identities are very hard to shake off because irrespective of our efforts to disown them, others may continue to identify us by those very markers of belonging. Such ascriptive identity is the most deterrant to self-realisation. Expanding and overlapping circles of community ties i.e. family, kinship, caste, ethnicity, language, region or religion give meaning to our world and give us sense of identity, of who we are.

Question 7.
What is Self-reflexivity?
Answer:
Sociology can show us what we look like to others. It can teach us how to look at ourselves from outside, so to speak. It is called “Self-reflexivity’ or sometimes just “Reflexivity’.

Question 8.
‘Sociology can help us to map the links and connections between ‘personal troubles’ and ‘social issues’. Discuss.
Answer:
C. Wright Mills a famous American Sociologist has mentioned, “Sociology can help us to map the links and connections between personal troubles and social issues.” As far as personal troubles are concerned Mills means the kinds of individual worries, problems or concerns that everyone has.

Question 9.
How colonial rule facilitated Indian consciousness to emerge? Discuss.
Answer:
1. Colonial rule unified all of Indian for the first time politically and administratively.
2. Colonial rule brought in the forces of modernization and Capitalist economic change.
3. However this economic, political and administrative unification of India under colonial rule was got at great expense.
4. Colonial exploitation and domination scared the whole Indian society in different ways.
5. Colonialism also gave birth to its own enemy—nationalism. The concept of modem Indian nationalism took shape under British Colonialism.
6. The rampant exploitation and the shared experience of colonial domination helped unity and exercise different sections of the Indian society. It also created new classes and communities. The Urban middle classes were the prime carrier of nationalism.

Question 10.
What steps were taken by colonial rules for the smooth functioning of its rule?
Answer:
The steps taken by colonial rules for the smooth functioning of its rule were that they:

• Used new mechanical techniques in production.
• Started new market system in trade.
• Developed means of transport and communication.
• Formed bureaucracy based on civil service of all India nature.
• Established formal and written law.

Question 11.
Which social reformers carried out social reform movements during the British colonialism in India?
Answer:
The prominent leaders of the reform movements were Raja Ram Mohan Roy, Ishwar Chandra Vidyasagar, Dayanand Saraswati, Bal Gangadhar Tilak, Mahatma Gandhi and others.

Question 12.
State the processes the began during the British colonialism in India.
Answer:
This was the period when modem period began in India and the external forces of modernization, westernization, industrialization entered.

Question 13.
State main differences between Sociology and other subjects.
Answer:
1. Sociology is a subject in which no one starts from Zero, as everyone already knows about society. However, other subjects are taught at school, at home or elsewhere.

2. Being an integral part of the process of growing up, knowledge about society seems to be got naturally or automatically.
In case of other subjects, no child is expected to already know something.

3. It means we know a lot about the society in which we live and interact.As far as other subjects are concerned, prior knowledge is almost negligible.

4. However, this prior knowledge or familiarity with society is both an advantage and disadvantage for sociology.
In the absence of prior knowledge there is no question of advantage or disadvantage in case of other subjects.